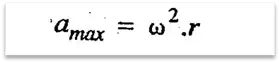For Velocity and Acceleration of a Particle Moving With Simple Harmonic Motion (SHM), consider a particle, moving round the circumference of a circle of radius r, with a uniform angular velocity ω rad/s, as shown in Fig. 1.32. Let P be any position of the particle after t seconds and θ be the angle turned by the particle in t seconds. We know that

          θ = ω.t, and x = rcosθ = rcosωt

The velocity of N (which is the projection of P on XX’) is the component of the velocity of Pparallel to XX’.

VN = v sinθ = ω.rsinθ

The velocity is maximum, when x = 0, i.e. when N passes through O (i.e. mean position).

vmax = ω.r

The acceleration of N is the component of the acceleration of P parallel to XX’ and is directed

towards the center O.

The acceleration is maximum, when x = r, i.e. when P is at X or X’.