CONIC SECTION mainly consists of three major parts they are

Ellipse

Parabola

Hyperbola

Conic sections are the intersections of a right regular cone, by a cutting plane in different positions, relative to the axis of the cone.

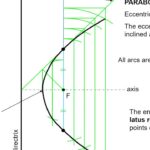
PARABOLA

The parabola  is a conic section, the intersection of a right circular conical surface and a plane to a generating straight line of that surface. Given a point (the focus) and a corresponding line (the directrix) on the plane, the locus of points in that plane that are equidistant from them is a parabola.

CONSTRUCTION 

ELLIPSE

an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is perpendicular to the axis. An ellipse is also the locus of all points of the plane whose distances to two fixed points add to the same constant.

Ellipses are closed curves and are the bounded case of the conic sections, the curves that result from the intersection of a circular cone and a plane that does not pass through its apex; the other two (open and unbounded) cases are parabolas and hyperbolas. Ellipses can also arise as images of a circle under parallel projection and some cases of perspective projection.

HYPERBOLA

It is similar to parabola which has he eccentricity greater than 1