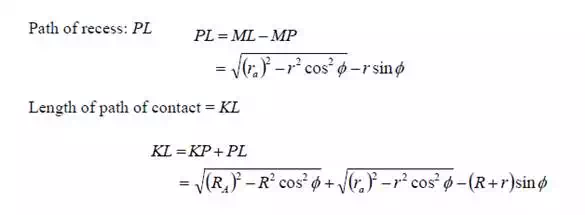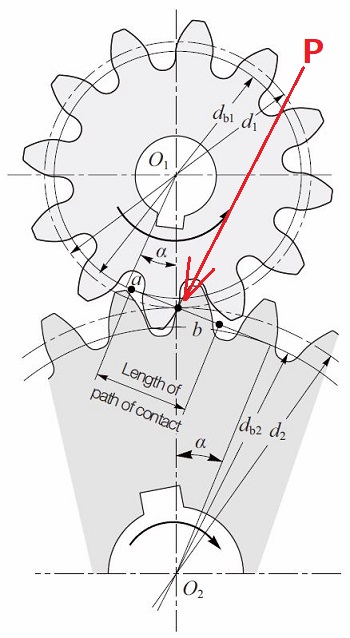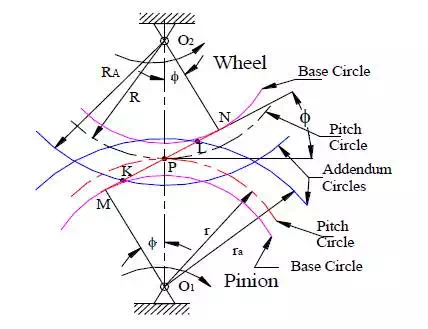
Consider a pinion driving wheel as shown in figure. When the pinion rotates in clockwise, the contact between a pair of involute teeth begins at K (on the near the base circle of pinion or the outer end of the tooth face on the wheel) and ends at L (outer end of the tooth face on the pinion or on the flank near the base circle of wheel).

MN is the common normal at the point of contacts and the common tangent to the basecircles. The point K is the intersection of the addendum circle of wheel and the common tangent. The point L is the intersection of the addendum circle of pinion and common tangent.

The length of path of contact is the length of common normal cut-off by the addendum circles of the wheel and the pinion. Thus the length of part of contact is KL which is the sum of the parts of path of contacts KP and PL. Contact length KP is called as path of approach and contact length PL is called as path of recess.

r_a = O₁L  = Radius of addendum circle of pinion,and

R _A = O₂K = Radius of addendum circle of wheel

r = O₁P = Radius of pitch circle of pinion,

and R = O₂P = Radius  of pitch circle of wheel.

Radius of the base circle of pinion = O₁M = O₁P cosf = r cosf

and radius of the base circle of wheel = O2N = O2P cos f  = R cosf

From right angle triangle O₂KN