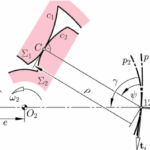
For a constant velocity ratio, the position of P should remain unchanged. In this case, the motion transmission between two gears is equivalent to the motion transmission between two imagined slip-less cylinders with radius R₁ and R₂ or diameter D₁ and D₂. We can get two circles whose centers are at O₁ and O₂, and through pitch point P. These two circles are termed pitch circles. The velocity ratio is equal to the inverse ratio of the diameters of pitch circles. This is the fundamental law of gear-tooth action.

The fundamental law of gear-tooth action may now also be stated as follow (for gears with fixed center distance)

A common normal (the line of action) to the tooth profiles at their point of contact must, in all positions of the contacting teeth, pass through a fixed point on the line-of-centers called the pitch point.

Any two curves or profiles engaging each other and satisfying the law of gearing are conjugate curves, and the relative rotation speed of the gears will be constant(constant velocity ratio).