The notion of a quantum dot [1–3] comprises various nanometre-size semiconductor structures, manufactured by means of different technologies and resulting in special limitations on the carrier dynamics (electrons and holes), as well as excitations of electron-hole pairs (excitons). The Coulomb energy scales withe QD size d as 1/d (and is of the order of meV for QDs), while kinetic energy scales as 1/d2, which leads to the shell properties of dots, distinct in comparison to atoms (more complicated Hund-type rules for QDs), since both energies remain within mutual proportions of d, which favours Coulomb energy for dots in contrast to atoms [1] at the scale of meV orders. The nanometre-scale limitations on quantum dynamics result in kinetic energy quantization,

In the case of QDs, quantization energy locates thus within a range accessible for control by means of external fields (electric and magnetic), in contrast to atoms (for the latter, quantum state control by means of external fields requires such values that are beyond the reach of present technologies). This advantage of QDs—which are relatively easy to create due to a variety of existing technologies in addition to their parameters’ flexibility and the possibility of immersing them in various media or even creating or modifying them by means of external fields—makes them very promising objects of new nanotechnologies and spintronic practical projects. Various semiconductor materials may be used to create QDs. Note that insulator or metallic nanoparticles are also manufactured (however, collective electron liquids in metallic nanoparticles manifest distinct physical properties in comparison with semiconductor QDs, which explains why metallic nanostructures are not called QDs). For opto-electronic use, semiconductor dots seem best-suited due to their localization within other nanostructures (e.g., in quantum wells), with well-established technologies for control over such systems. Semiconductor QDs may be manufactured by means of etching technologies after a high-resolution photolithographic process (with the use of an ion or electron beam) has been applied (ordinary optic lithography with a resolution of up to 200-300 nm is not sufficient). Other technologies used here include among others the Stransky-Krastanov dot self-assembling method consisting in the application of epitaxy layers by MBE or MOCVD [MBE, Molecular Beam Epitaxy; MOCVD, Metal Organic Chemical Vapour Deposition]. Various lattice constants in successive epitaxy layers result in the spontaneous creation of nanocrystals on the ultra-thin so-called ’wetting layer’. Electrical focusing in a quantum well [1, 4, 5] consists of yet another promising technique which, despite being at an early stage (due to a lack of sufficiently precise electrodes), offers the highest dot parameter flexibility and allows for dots to switch on/off within the working time periods of devices based on them [1, 4–6].
The possibility of control over the quantum states of carriers in QDs and their coherent (deterministic, controllable) time evolution are vital for nanotechnological and spintronic applications (especially where this concerns so-called ’single-electron’ or ’single-photon’ devices) as well as for the quantum processing of information. The absence of decoherence or its significant reduction up to the lowest possible level, at least within the time periods of control realization, is essential for all these applications. However, decoherence is unavoidable due to irreducible dot-environment interactions (there is no means of a dot’s total isolation). In the case of nanostructures, QDs offer a new class of physical phenomena within the decoherence and relaxation range, entirely distinct from analogous processes in bulk materials or in atomic physics. This is due to the characteristic nanoscale-confinement energy, reaching values close to the typical energy parameters of crystal collective excitations (the energy characteristics of band acoustics and optical phonons). This convergence of energy scales results in resonance effects, which is different from what is observed in atomic physics where the scale of the atom-confinement energy is three orders of magnitude higher than the energy of crystal collective excitation, resulting in the weak influence of phonons on atomic states (included as a very small perturbation only). Specific decoherence effects in QDs result from a strong (resonance) coupling effect between the carriers trapped in them and the sea of various types of phonons (as well as with other collective excitations, or with local degrees of freedom, e.g., related to admixtures). This is why the frequently-used notion of an ’artificial atom’ in reference to QDs is, to some extent, misleading. The same reasons are responsible for the fact that QD modeling which does not account for environment-induced collective degrees of freedom may give rise to false conclusions since significant hybridization-induced (decoherence) changes of energy levels can reach up to 10%. This reduces the modeling fidelity if the environmental effects are neglected. Therefore, the current physics of nanostructures should embrace the recognition of the complex decoherence and relaxation effects observed in QDs for trapped carriers’ spin and charge, which are essentially different from what is observed in bulk materials and atoms.
Limitations on the quantum processing of information
Unavoidable decoherence—uncontrolled quantum information leakage into the surrounding environment due to the system’s interaction with the environment—perturbs the ideal quantum procedures which ensure the running of quantum schemes [7–12]. If, however, decoherence is kept below a certain threshold, quantum error corrections can be made by applying so-called ’quantum error correction schemes’ [13], which enables the realization of any quantum procedures of a quantum computer or any other deterministic quantum project.In classical information processing, quantum error correction consists in multiplying classical information and verifying by comparison the multiplied (redundant) classical registers with arbitrary frequency, errors which appear from time to time are identified and corrected immediately. In the quantum case, the multiplication of quantum information is impossible (No-Cloning theorem) and quantum error correction is based on a different scheme:
• Seeking more decoherence-resistant areas of the Hilbert space (multi-qubit states which, in a pair of qubits, record symmetrically both “true” and “false” are decoherence-resistant, e.g., singlet-type qubit states; information (or quantum states) symmetrization requires, however, the multiplication of quantum registers, which makes decoherence rise exponentially).
• Attempting the replacement of an information carrier for a more decoherence-resistant one (e.g., temporarily, a state can be teleported onto a more resistant carrier).
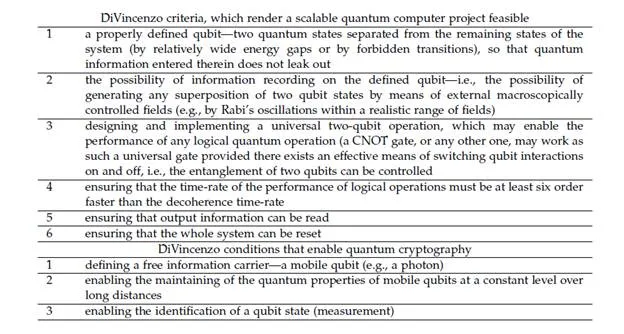
In order to satisfy quantum error correction requirements, DiVincenzo formulated a set of conditions [7, 14–16] which allow for the possibility of the implementation of quantum error correction (the typical decoherence time must be at least of six orders longer than the typical times of quantum procedures). None of the currently suggested solutions for quantum computers have satisfied these time restrictions. This situation may follow from the fact that the same interactions which allow for qubit control (logical operations) are also responsible for decoherence. The stronger (energetically) the interaction is, the faster the logical operations can be carried out. However, the same interaction couples the system with the surrounding environment and produces strong decoherence effects. In nanotechnological and optical projects involving quantum computers (multi-qubit), the difference in the time-rate of quantum operations in relation to decoherence still do not exceed three orders of magnitude.
However, it is expected that further intensive research in this area should result in:
• Finding another method of quantum error correction (despite great efforts, there is still no relevant solution).
• Finding a combined solution with qubit conversion (between a fast, controlled carrier and a decoherence-resistant one—unfortunately, qubit conversion is
also inconveniently long-lasting).
• Finding global, topological and thus decoherence-resistant carriers of quantum information in them.
• Braid groups (and non-Abelian anyons)—herein, the durations of logical operations are expected to be of 30 orders of magnitude greater than those
of decoherence processes [17] (however, this is still unclear and it is doubtful if it is experimentally viable).
• It is hoped that superconductive states may satisfy the DiVincenzo conditions as they have non-local properties to a significant extent.
In the case of quantum cryptography, equipment requirements [18] are more easily met in respect to decoherence and this is why this quantum technology (public key distribution via a quantum channel) has been used in practice in optical systems [fibre-optical ones over distances of 100 km (up to 1000 km), and outdoors over distances of 2 km].
Quantum dots—the prospective technology for quantum gates
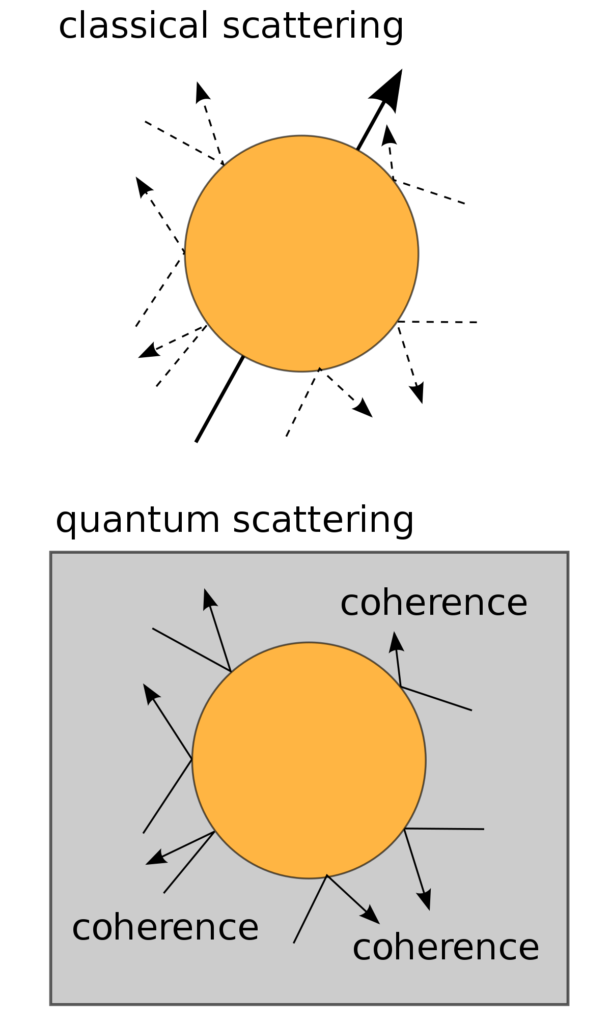
The idea of employing quantum evolution for information processing corresponds with the feasibility of the deterministic control over a quantum system in order to execute a previously designed quantum algorithm. However, such a deterministic evolution (also called ’unitary’ or ’coherent’) requires a totally isolated quantum system. Unfortunately, no quantum system can be totally isolated from the environment. Any quantum system is susceptible to the environment’s influence. In consequence, unitary or coherent evolution is perturbed, and quantum information undergoes uncontrollable and irreducible leakage into the environment. Therefore, the feasibility of the construction of a scalable quantum computer is seriously hindered due to decoherence phenomena. The better recognition of decoherence processes in quantum systems may, however, enable the development of new technologies transcending these limitations and facilitating the attainability of quantum gates. Quantum state decoherence progresses along two channels: relaxation, i.e., quantum state annihilation; and dephasing, i.e., phase relations change within a quantum state description. Relaxation (or ’amplitude decoherence’) is related to the decrease in time of the diagonal elements of the quantum state density matrix, whereas dephasing (or ’phase decoherence’) corresponds to the reduction of the off-diagonal elements of the density matrix. Both types of decoherence are caused by interaction with the environment and they become more significant the stronger the interaction is. Solid-state technology (which is promising for new practical realizations of the quantum processing of information using nanometre-scale semiconductor QDs) is burdened mostly with phase decoherence processes. Both the charge (i.e., orbital) and the spin degrees of freedom of quantum states in QDs undergo dephasing due to their environment (however, it should be emphasized that the spin degrees of freedom seem to be more decoherence-resistant than orbital degrees of freedom, since they are less susceptible to direct crystal phonon-induced interaction; however, spin requires much longer periods of time-control than orbital degrees of freedom due to weaker interaction with spin).
Below we present a decoherence analysis, in particular the phase decoherence of the charge (orbital) degrees of freedom and degrees of freedom of spin of excitations localized in QDs, dealing with the issues associated with limitations on the feasibility of QIP. In the case of semiconductor QDs, decoherence is unavoidable due to strong dot-environment interaction (there are no means for the perfect isolation of a dot). In the case of nanostructures—QDs included—there appears to be a new class of physical phenomena related to decoherence and relaxation, distinct from analogous processes in bulk materials and atomic physics. This is due to characteristic meV-scale energy resulting due to nanoscale confinement, reaching values close to the typical energy parameters of band phonons in the surrounding medium. This coincidence of energy scales results in resonance effects, which is different from what is observed in atomic physics. For atoms, the incommensurability of the atom-confinement energy and phonon energy is of three orders of magnitude, resulting in a weak phonon impact on atomic states. Specific decoherence effects in QDs result from strong and resonant coupling between the carriers trapped in dots and the sea of various types of collective excitations in the surrounding medium, which highly modifies the QD states. Hybridization-induced changes of energy levels reach up to 10%. Therefore, the decoherence and relaxation effects observed in QDs and for trapped carrier spin or charge (which are essentially different from what is observed in bulk materials and atoms), seem to be of central importance for any possible QD applications, including QIP.
Phase decoherence of orbital degrees of freedom in nanostructures
Orbital degrees of freedom pertain to charge-type excitations, such as electrons and holes and charge-balanced electron-hole pairs—excitons. As charge carriers, these excitons interact with the electric field of the electromagnetic wave and so they can be controlled by means of quantum optics methods. Charge-type excitations can be localized in nanometre-scale artificial structures manufactured within various semiconductor heterostructures, namely in QDs. Excitons attract special interest as they can be precisely controlled by an electromagnetic wave within the visible (or near infrared) light range corresponding to the typical energy gap separating electron states from hole states in semiconductors (a typical material is GaAs and QDs will be, e.g., self-assembled structures of GaAs/InAs type). By accommodating the energy of (incident light) photons with the energy of the exciton, an exciton state in the Rabi oscillation regime can be created in which the superposition state of the charge qubit spanned on the states |1 > (no exciton in a QD) and |2 > (one exciton in a QD) can be selected. The techniques of ultra-high-frequency laser impulses (measured in femtoseconds) and the resulting application of a high intensity beam allowing for high-frequency Rabi oscillations [19] has attracted a lot of interest in QIP research. This interest has been centred on the fact that the lifetime of the excitons in the dots is measured in nanoseconds (this may suggest a difference of six orders of magnitude between the control time and the amplitude decoherence time, which is required by DiVincenzo’s criteria [7, 13–16, 20]). Nevertheless, in QDs the interaction between the excitons (electrons and holes) and phonons of the surrounding crystal is unavoidable and must be accounted for in all considerations, thus diametrically changing this ostensibly convenient situation. Phonons are quanta of the crystal oscillations; acoustical phonons refer to the oscillations of the density type (all the atoms in the unit cell oscillate in the same direction) and optical phonons are related with polarization oscillations (the opposite-sign ions in the unit cell oscillate in the opposite directions; polarization oscillations in such ionic crystals can be excited by means of light, and thus they are called ’optical’ phonons). Both types of phonons can interact with charge-type degrees of freedom in QDs. Phonons can be of transversal or longitudinal polarization, but these are the longitudinal modes (LO and LA for optical and acoustic phonons, respectively) that contribute most substantially to the interaction with the electrons/excitons [21].
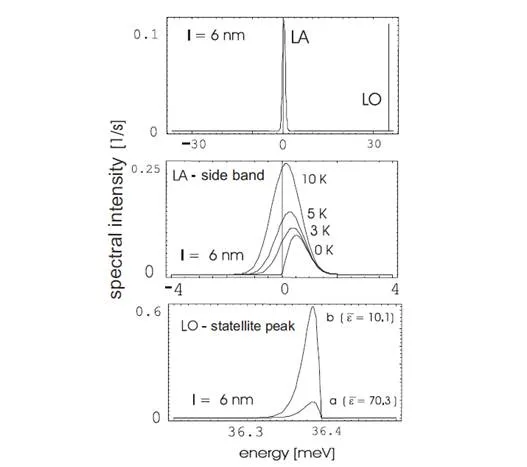
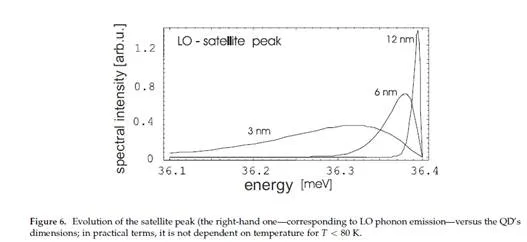
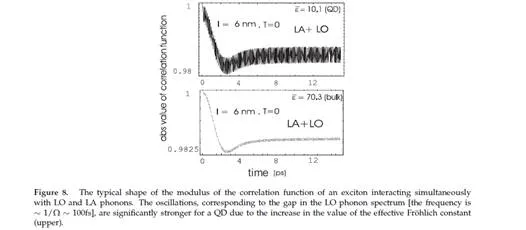
In polar materials (e.g., GaAs, a weakly polar semiconductor), LO phonon interaction prevails. The interaction of charges with LO phonons is characterized by means of the dimensionless Fröhlich constant [21, 22]. The higher the constant value, the stronger that the interaction is between the charges and the LO phonons, and for the semiconductor GaAs three-dimensional (bulk) the constant averages out at around 0.06. For QD GaAs/InAs, experiments (infrared absorption in a magnetic field and the broadening of the satellite luminescence peak connected to LO phonons, expressed quantitatively via the so-called ’Huang-Rhys factor’ [23]) show a double value of the constant, which suggests a substantial increase of the interaction with LO phonons. This phenomenon has been explained [24] with regard to a certain ambiguity [21] in the definition of LO phonon-electron interactions in crystals. The interaction between an LO phonon and an electron leads to the polarization of the crystal lattice by the moving electron. This polarization (i.e., an appropriate packet of optical phonons) is dynamic and leads to a reverse interaction with the polarization-inducing electron. It can be thought of as being composed of two components: an inertial one, which lags behind the moving electron; and a non-inertial one, which accompanies the moving electron. The latter component should be contained in the total crystal field which defines the electron itself (the electron in the crystal is not a free particle and includes, by its definition, the periodic crystal field—thus it can be characterized by the effective mass and quasi-momentum instead of momentum). The necessity of extracting only the inertial part of the polarization from the total interaction of the electron and the LO phonons leads to the above-mentioned ambiguity in the definition of the electron-LO phonon interaction. When the electron is trapped in a QD, it moves with a quasi-classical velocity [25] which exceeds the velocity of a free band electron. Thus, it better escapes from the dynamic polarization, which results in an increase in the inertial part of polarization and the interaction between the electron and LO phonons in QDs. The more localized the electron in a smaller QD, the bigger the quasi-classical velocity of the electron and the bigger the increase in the interaction with LO phonons. The quantitative analysis of the problem agrees well with the experimental data. It should be emphasized, however, that the marked increase in the value of the Fröhlich constant in QDs parallels the increase in the decoherence of electron/exciton states in dots due to the increase in the interaction between the small system of the QD and the sea of LO phonons in the crystal.
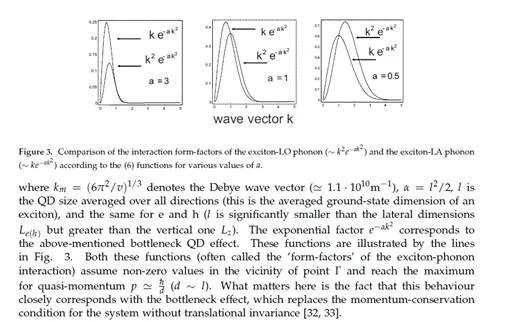
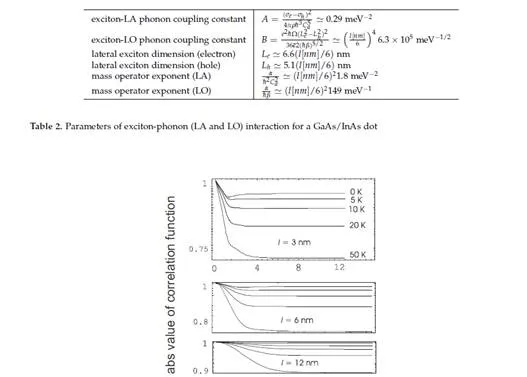
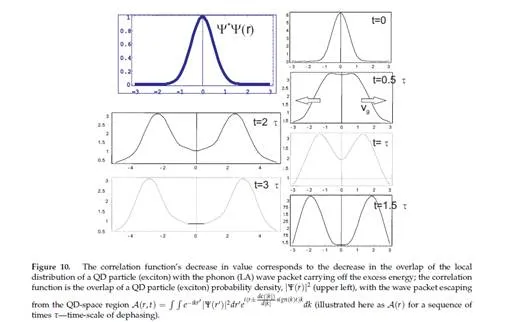
The energy scale corresponding to the nanometre localization of electrons (excitons) in QDs ranges from a few to several tens of meV. The same energy scale also characterizes the phonons in crystals, in which the energy of LA phonons ranges from 10 to 20 meV at the edge of the Brillouin zone and the energy of LO phonons at the centre of the Brillouin zone (a gap in the LO phonon spectrum at point Γ [21, 22]) reaches 30 meV. Thus, in the case of QDs we deal with a strong coupling regime for an interaction of QD charge degrees of freedom with phonons (of all types). The same energy scale of both types of excitations—local in QDs and collective in the surrounding crystal—results in the strong mutual hybridization of these excitations or in the dressing of electrons (holes) or excitons with phonons and in the creation of composite particles (quasi-particles)—polarons [21, 22, 26–29]. The creation of polarons in QDs is a strongly decoherent process (much more than it is in bulk materials). The dynamics of this process can be investigated by employing the Green function technique [28]. By means of this technique, the correlation function of the exciton (electron) in the QD can be expressed, which defines the overlap (the scalar product) of the state of the carrier gradually dressed by phonons with the initial state of the bare exciton (or electron) in the dot. Thus, it is possible to quantitatively characterize the leakage of quantum information (fidelity loss) due to the entanglement (in a quantum sense) of the QD’s charge with the deformation and polarization degrees of freedom of the whole crystal, which are entirely beyond our control.
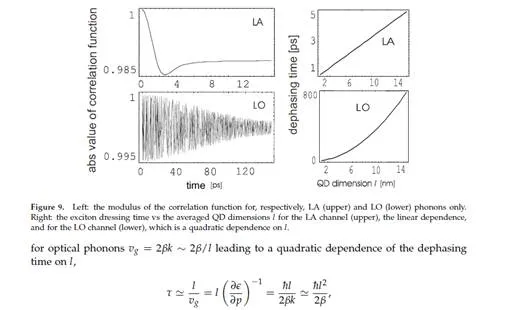
The inertia of the crystal lattice is so disadvantageous that it makes it impossible to maintain the coherence of orbital degrees of freedom dynamics (the unitary quantum evolution of the excitations) within the time periods required by the DiVincenzo conditions. The typical times of dressing charge-type excitations with phonons are located within the time-range of single picoseconds, which is the middle of the six-orders time window between the amplitude decoherence time for excitons in QDs and the time-scale of the quickest techniques for their excitation. On both sides of this window, there appear windows of three-orders of magnitude, which precludes the implementation of the quantum error-correction scheme due to the non-fulfilment of the DiVincenzo conditions. These strongly unfavourable estimations indicate that it may be impossible to scale a quantum computer in a QD technology with only by light control unless more effective quantum error-correction schemes would be proposed [7, 13, 14].
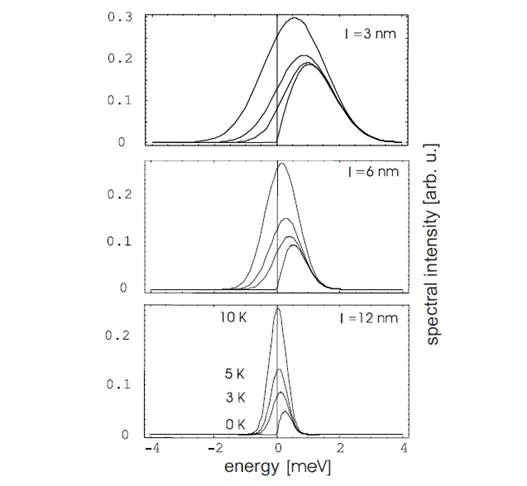
It should be emphasized that LA phonons are of greater importance to the process of dressing the excitons with phonons (polaron decoherence effects), despite the fact that their interaction with excitons is energetically much weaker (at least by one or two orders of magnitude) than in the case of LO phonons. Strong dephasing due to LA phonons corresponds with a wide linear dispersion of acoustic phonons, which in turn leads to a more immediate and significant induced change in the wave functions of charge-type excitations in QDs than in other phonon modes.LA phonons-induced decoherence (phase decoherence or dephasing, corresponding to the reduction of the off-diagonal elements of the density matrix [8–12]) is—and as can be shown by means of a microscopic analysis—a relatively fast process and its time-scale is of the order of the ratio of the dot diameter and the sound velocity (it is of the order of picoseconds). Acoustic phonons are especially inconvenient as they are present in any crystal (as well as in any amorphous material), and this is why the above-presented mechanism of decoherence is unavoidable by its nature [strong dephasing also exists at a temperature of 0 K due to phonon emission; at higher temperatures, the dephasing effects are enhanced due to phonon absorption effects, which become more important with the increase in temperature].Strong decoherence restrictions on the quantum evolution of the charge degrees of freedom in QDs encouraged the researchers to concentrate their attention on the spin degrees of freedom in nanostructures (spin does not interact directly with phonons) instead of pursuing the idea of constructing an quantum computer based on QDs that is only controlled by light [7, 14, 28].
Phonon-induced dephasing of excitons localized in quantum dots
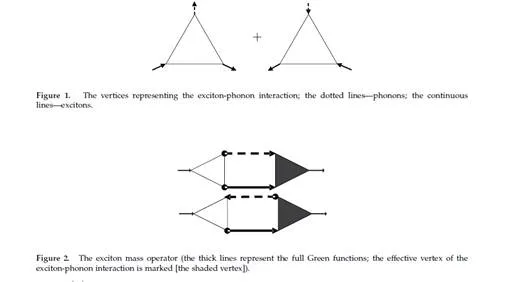
An exciton created in a QD by means of an non-adiabatic process (in the sub-picosecond order) [4, 5, 30] is a bare particle (an electron-hole pair) which is gradually dressed with phonons until it becomes a polaron. The time within which the polaron is created depends upon the lattice inertia. It is relatively long and its accurate evaluation is an important task. The process of the hybridization of a QD-localized exciton with the collective excitations of the crystal lattice surrounding the QD is, in fact, a time-dependent evolution of a non-stationary state, which at the initial time (the moment of the excitation’s creation) is identical with the state of the bare exciton. The bare exciton is not the stationary state of the whole system, the QD exciton and the sea of phonons in the surrounding crystal interacting with it (a polaron represents a stationary state of such a complex system). The non-stationary initial state (the bare exciton) [the electric field of the e-m wave interacts with the charge and, in consequence, excites a bare electron from the valence band into the QD; the resulting hole is also captured by the QD—a bare QD exciton is thus created] undergoes further non-stationary evolution. In the non-stationary state, the energy is not determined; however, the mean energy is shared over time between the subsystems, the QD and the phonon sea. The mean energy of a bare QD exciton is higher in comparison with the polaron energy (whose energy is lower and therefore the polaron is created by means of interaction with phonons due to energy minimization). The excess energy of the lattice deformation (for acoustical phonons) together with the polarization energy (for optical phonons) is carried outside the QD by the LA and LO phonons, respectively (by their wave packets). A QD polaron is created—a hybridized state of an exciton dressed with an LA and LO phonon cloud [actually, the name of the polaron refers to electrons dressed with LO phonons [22]—a process dominating in strongly polar materials; here, the name refers generally to an electron or exciton dressed with all types of phonons]. The time-scale of QD polaron creation is of the same order as the time that a phonon-wave packet needs to leave the QD area. It should be emphasized that this process is not to be interpreted in terms of Fermi’s golden rule [in such an approach, quantum phase transitions resulting from a time-dependent perturbation refer to transitions between stationary states, which is not the case here] [25]. The process of polaron creation is a non-stationary state evolution, in which the elementary processes of phonon absorption or emission contribute in the virtual sense (without energy conservation). Note that the polaron energy is shifted with respect to the bare QD exciton energy by a few meV [28], while the LO phonons energy has a much greater gap, h¯ Ω ‘ 36, 4meV (in GaAs). The kinetics of polaron creation correspond with the coherent evolution of an entangled state of two interacting systems, namely a QD exciton and the sea of phonons (of various types), and this state in non-separable [28].
The exciton-phonon system is represented by the following Hamiltonian:










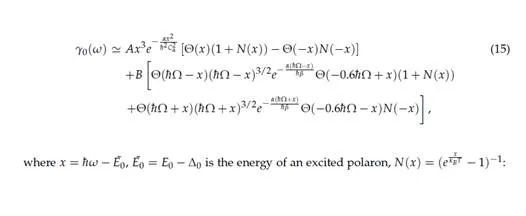








Decoherence of the degrees of freedom of spin in quantum dots
Spin do not interact directly with with phonons—the spin of the QD excitations interacts weakly with the lattice oscillations due to their links to orbital (charge) degrees of freedom via:
• spin-orbit coupling [43],
• specific Hund-like rules for multi-electron QDs [1]—the filling of the subsequent shell in the multi-electron QD depends upon the total electron (hole) spin of a given shell [the generalization of singlet and triplet states] which, in effect, link spin and orbital degrees of freedom.
Weak spin coupling with phonons suggests that the spin of a QD electron constitutes a well-isolated quantum system (an insignificant spin-orbit interaction results in an extremely slow spin decoherence, the same is due to weak interaction with nuclear spin) that is suitable for a qubit’s definition. One can expect that for spin qubits in QDs, DiVincenzo’s conditions would be satisfied [7, 14, 15]. Due to the minor influence of the surrounding medium, the QD’s spin coherence is maintained until the time period of order of µs [16]. However, a difficulty arises when Rabi oscillations are implemented (for single qubit operations). Because of the low value of the gyromagnetic factor in semiconductors, qubit spin control (a qubit spanned across two spin orientations in an external constant magnetic field) via Rabi oscillations is extremely slow and the DiVincenzo conditions are again not satisfied (the Pauli term, gµBszB, leads to very slight Zeeman splitting of only 0.03 meV/T, in GaAs)
For two-qubit operations of spin qubits, no such disadvantage exists—there is an effective procedure for switching spin qubit interactions on and off [15, 16] resulting in qubit entanglement control at the time-scale of picoseconds. The idea of spin interaction control follows from the phenomenon of exchange interaction between two spins, being induced by strong Coulomb interaction [44]. The exchange energy for it is the singlet-triplet energy gap for the spin pair [44], and consequently it is of (several) meV in magnitude, resulting in a picoseconds time-scale for the control of the entanglement of qubits. The scheme of this control relies upon the singlet and triplet states of an electron pair (each electron captured in an individual QD but located closely enough to maintain their quantum indistinguishability [their localized wave functions must overlap]) and their relation with the orbital structure of the corresponding wave functions. Due to the fermionic nature of electrons:





Dephasing induced by the dressing of QD exciton spin with magnons in a diluted magnetic semiconductor’s surroundings
An interesting question arises with regard to the QD spin in the magnetic surroundings when the Pauli term causing the Rabi oscillations for spin can be strengthened due to an increase in the effective gyromagnetic factor. Spin does not interact directly with phonons, and thus it is free from phonon-induced dephasing. Nevertheless, the dephasing role of phonons may be played by spin waves in magnetically-ordered media which, on the other hand, are convenient for accelerating single-qubit QD spin control to the level required by the DiVincenzo conditions. Spin waves (frequently called ’magnons’) are collective spin-type excitations in the ferromagnetic or anti-ferromagnetic medium (or in any other magnetically-ordered spin system), and possess similar band properties to phonons in crystalline structures. The spin-exchange interaction between the magnons and the local QD spin (of an exciton trapped in a QD) is relatively strong and causes the dressing of the QD spin with the magnons in a similar fashion to the dressing of the QD charges with phonons. The opportunity for the experimental study of such a spin dressing phenomenon may be linked to the so-called ’diluted magnetic semiconductors’ of the type III-V (e.g., Ga(Mn)As) or II-VI (e.g. Zn(Mn)Se). In these magnetically and weakly doped semiconductors, some relatively small part of the cations (usually a few %) is randomly substituted by transition metal ions (typically of Mn). The admixture spins interact with the spins of band holes and as a result the ferromagnetic ordering of the admixture spins is observed. The related Weiss field enhances the effective gyromagnetic factor in the Pauli term, describing the spin action of the external magnetic field conveniently for the acceleration of the control over the local QD spin.
Spin waves in the diluted magnetic semiconductor
To describe the dephasing of QD spin caused by magnons in DMSs quantitatively, the analytical expression of the spin wave spectrum in the DMS is needed. This can be found in the paper [64]. For the relevant theoretical description of the spin subsystem of the DMS, the model of dopant spin exchange mediated by band holes is utilized [58, 59], assuming












Conclusions
In conclusion, we can state that in the case of QDs we deal with a specific type of phonon-induced phenomenon, which is essentially distinct from the phonon-induced effects in bulk semiconductors. This difference is caused by the compatibility of the energy scale for carriers trapped in QDs with the band-phonon energy scale. Owing to this energy coincidence, the coupling of carriers in QDs with phonons always meets its strong regime limit. This coupling cannot be treated perturbatively, in general, and the resonance effects are of primary importance, resulting in strong polaron-type modifications of the QD electron and exciton spectra. The typical energy shift due to the formation of electron-polaron is of the order of 10%, while for exciton-polaron it is of the order of 5% with respect to the bare energy levels in QDs treated as separated from the environment. The confinement of carriers, as in the case of QDs, also causes the significant enhancement of the effective Fröhlich constant due to non-adiabatic effects, which additionally strengthens the electron-LO phonon interaction. The dressing of the electrons/holes/excitons in QDs with band phonons from the surrounding crystal induces the dephasing of charge (orbital degrees of freedom) in QDs (the off-diagonal decoherence). The typical time-scale of this dressing process in the case of the formation of an exciton-polaron in QDs turns out to be of the one picosecond time-scale (for a typical QD of 10 nm diameter). This dephasing is caused by the exciton dressing with LA phonons. Worth noting is the observation that the dephasing due to LO phonons is considerably smaller and slower—of the 100 ps scale. This phenomenon is caused by the relatively weak LO phonon dispersion near the Γ point (in the Brillouin zone), in contrast to the dispersion of LA phonons. Nevertheless, the outflow of the excess polarization energy to the space region outside the QD, as a typical process during LO polaron formation, is eventually accelerated by the anharmonic coupling (LO-TA is the most important anharmonic channel in GaAs), which results in a few ps time-scale. It is important to note that these effects of QD-charge dephasing by band phonons refer not only to QDs but also to all nanostructures in solids, because the carrier localization (the space-confinement of trapped carriers) plays the essential role here.
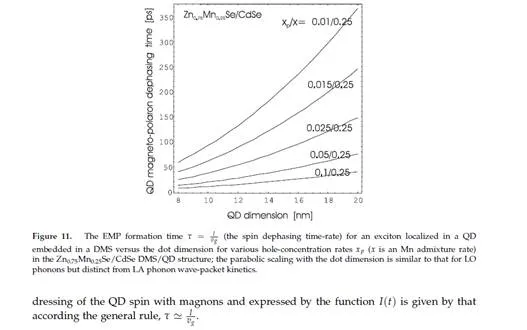
We have observed also that in magnetically-ordered media (like in DMSs), magnons (spin waves)play a similar destructive role to phonons. Spin waves cause the dephasing of the exciton spin in QDs, in a process of the formation of excitons-magnetos-polarons by the step-by-step dressing of the local spin of exciton in QD with the magnon cloud from the surrounding magnetically-ordered medium. By using the Green function technique, we have estimated the time for the dressing of the local exciton spin with band magnons in the case of DMSs which surround QDs by analogy to the dressing of QD charge (i.e., QD orbital degrees of freedom) with band phonons from the surrounding crystal. Nevertheless, the significant difference between these two phenomena is observed and elucidated, namely, in the case of spin dressing two magnons are needed (creation and annihilation) owing to the spin conservation in the interaction vertex, which results in the complete freezing (vanishing) of the spin pure dephasing at T = 0. This is in contrast to the phonon-induced pure dephasing, which maintains strong even at T = 0.The dephasing scheme for the exciton charge and spin in QD structures is important for the feasibility assessment of QIP implementations in QDs. The picoseconds time-rate for QD charge dephasing probably precludes the feasibility of the implementation of error-correction schemes for all optically-controlled gates in QD technologies. The dressing of a localized spin with magnons in a DMS (i.e., the time corresponding to the formation of EMP in a QD) takes place at a longer time-scale in comparison to dressing charges with phonons, and the related time-scale is of the order of 150-200 picoseconds due to the relatively weak quadratic magnon dispersion, similar to as was the case for LO phonons. Nevertheless, the time-rate for QD spin dephasing induced by magnons in the surrounding DMS is also inconvenient for QIP applications, similarly to the case of the dephasing of QD charges by phonons. The overall time-scale for QD spin kinetics (QD/DMS-embedded structures) is shifted by three-orders of magnitude to longer periods in comparison to QDs’ orbital degrees of freedom, though again with the same inconvenient dephasing time-rate falling right in the middle between the control-timing and the relaxation-timing (which does not allow the satisfaction of the DiVincenzo conditions). In this way, the ’three-orders time-limit’ caused by the dephasing phenomena is repeated for spin in the QD/DMS.
The pure dephasing of spin in QD/DMS structures disappears, however, at T = 0, and is strongly suppressed in amplitude at low temperatures (in contrast to the charge dephasing), which supports expectations of some advantages of spin degrees of freedom in QDs for QIP applications. that the p − d exchange between the band holes and the impure magnetic atoms may lead to the ferromagnetic alignment of the magnetic dopants (Mn). Note that the holes taking part in the spin exchange with the dopant Mn ions cause an indirect exchange beyond the weak, direct, short-range and anti-ferromagnetic exchange between the magnetic dopants [48]. The hole-induced indirect coupling, even for low concentrations of holes xp (lower than the magnetic dopant concentration x) occurs strong and leads to the ferromagnetic ordering of Mn spins even at relatively high temperatures, ∼ 110 K in Ga0.947Mn0.053As [58, 60]. Let is be emphasized that, in III(Mn)V DMSs, the Mn atoms of the magnetic dopants are simultaneously shallow acceptor centres, whereas in II(Mn)VI-type DMSs, the Mn dopants are not acceptors and the holes must be supplied by additional p doping. To briefly sketch the derivation of the magnon spectrum in DMSs, let us set out the Hamiltonian for the DMS system with magnetic dopants Mn2+ (with spin S = 5/2) in the form: