During  the  optical  excitation  of  carriers  in  a  semiconductor,  the  minimum  energy  re‐ quired  to  form  free  carriers  is  called  the  band  gap.  The  energy  below  that  value  cannot excite free carriers. However, low-temperature absorption studies of semiconductors have shown excitation just below the band gap [1]. This excitation is associated with the formation of an electron and an electron hole bound to each other, otherwise called an exciton. It is an  electrically  neutral  quasiparticle  like  in  a  hydrogenic  state.  At  low  temperatures,  the bound  states  are  formed  and  the  Coulomb  interaction  between  the  electron  and  the  hole becomes  prominent  [2].  The  negative  trion  (X-)  is  created  due  to  the  additional  electron bound to a pre-existing exciton and if a hole is bound to an exciton, a positive trion (X+) is created. Both the negative and positive trions are complex electronic excited states of the semiconductors and therefore, the 3-body problem is raised. Although Lampert [3] in 1958 originally and theoretically predicted the negative trion in semiconductors, K.Kheng et al. experimentally achieved a negative trion in Cd Te/Cd Zn Te quantum well [4]. The rapid progress of semiconductor technology in the recent years has allowed the fabrication of low dimension electronic nanostructures. Such nanostructures confine charged particles in all  three  space  dimensions.  In  low  dimensional,  especially  in  quantum  dots  [5,6]  (three dimension confinement), the picture is different because it is below a nanometer wide, a few nanometers thick, and in various shapes. The quantum confinement increases highly, and this quantum confinement leads to more stability of the excitons and trions by increasing their binding energy. The stability of such particles remains up to room temperature. A proper identification of the (X-) was not achieved until the early 1990’s in remotely doped, high-quality quantum-well (QW) structures [7-9]. Since then, extensive work has been carried out on (X-) inside the two-dimensional (2D) [wide quantum wells [7-11]] and quantum dots, which the first observations of the QD-confined charged excitons (trions) were performed on ensembles of the QDs [12]. There are many theoretical studies devoted to excitons [13-15] and trions [16- 25] in quantum dot. Most of such studies have treated and considered the spherical[26-28], lens shaped [29,30], square flat plated [31,32], and cylindrical [33,34] quantum dots.

In the present chapter, we study the influence of the 3-D quantum confinement on the binding energy of the exciton (X), negative trion (X-), and the positive trion (X+) in a semiconductor cylindrical quantum dot manufactured in GaAs surrounded by Ga1-xAlxAs. Using a variational approach and the effective mass approximation with finite confinement – potential. There have been  concerns  as  to  whether  the  effective  mass  approximation  could  still  be  valid  in  the quantum dot limit when the size of the exciton could be similar to the average lattice constants of bulk semiconductor [35].

Theoretical model

Within the effective mass approximation and non-degenerated band approximation, we can describe the exciton and trions in the following semiconductor structure: a symmetric cylin‐ drical QD of radius R and height L made of GaAs surrounded by Ga1-xAlxAs. In our model, the  electrons  and  the  holes  are  placed  in  the  external  potential  Ve(re, ze)  and  Vh (rh , zh ), respectively and coupled via Coulomb potential. We choose the potential in GaAs (well) to be zero and equals Ve  or Vh   in the barrier material.

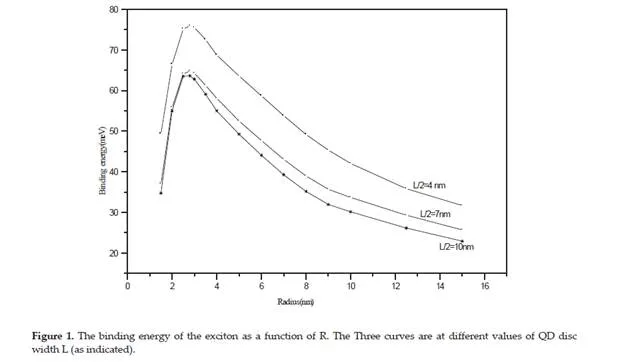
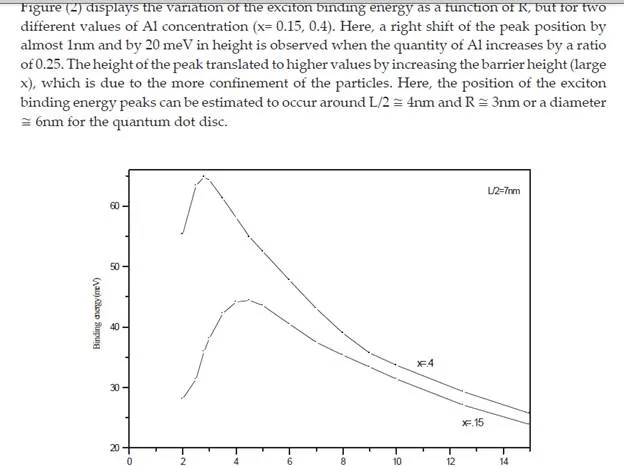
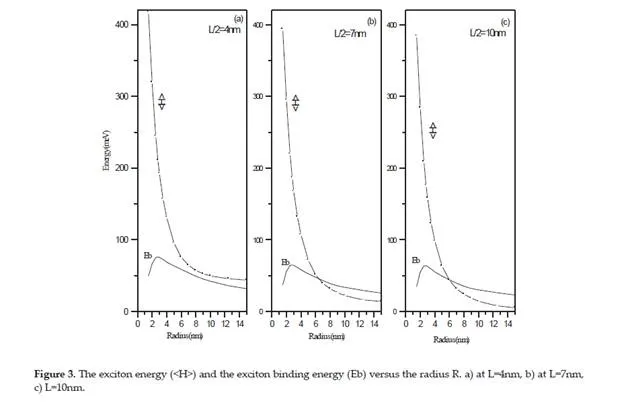
Conclusion

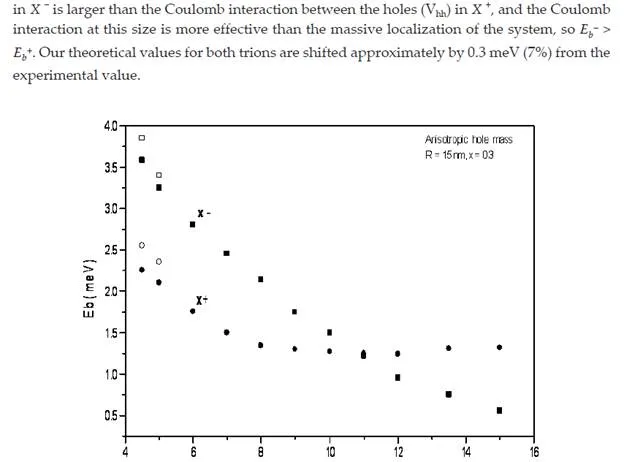
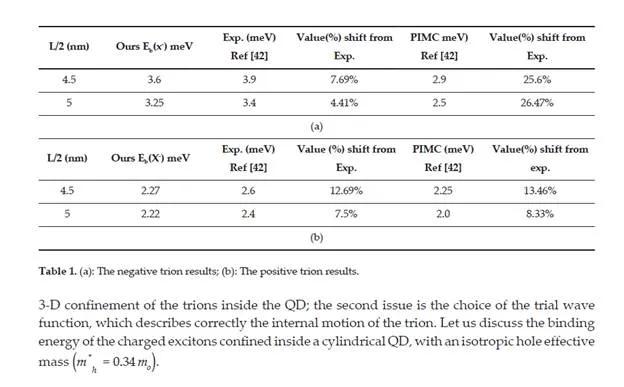
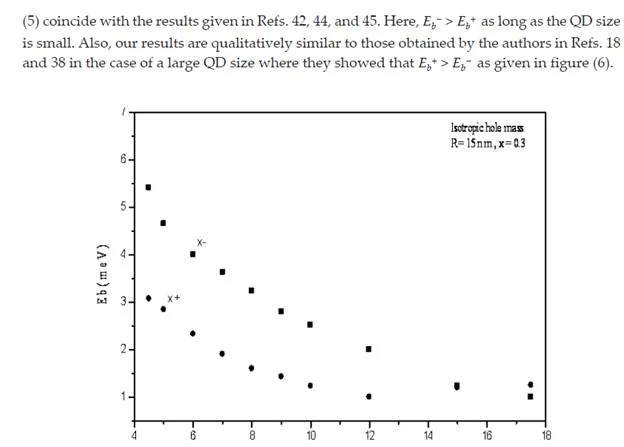
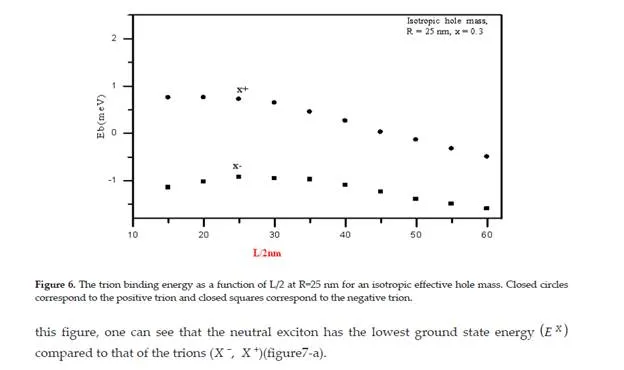
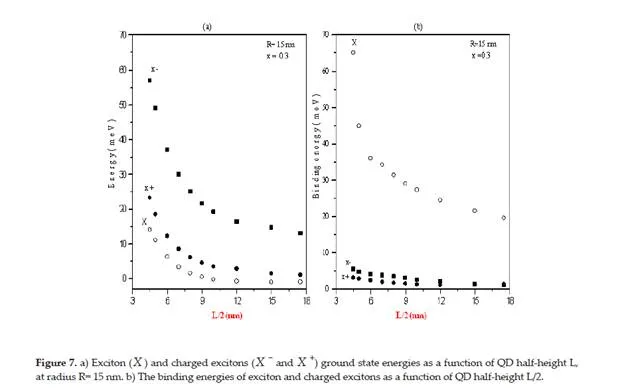
We have introduced a trial wave function for the positive and negative trions confined in a cylindrical QD. Using the given wave, we obtained a higher binding energy of negative trions than the positive trions inside the QD with a half-height less than the effective Bohr radius and we referred that to the high Coulomb interaction energy between the two electrons compared to the weak Coulomb interaction between two holes at such small QDs. When the half-height of the QD increased to values higher than the Bohr radius, the negative trion binding energy rapidly decreases than the binding energy of the positive trion. An anisotropic hole effective mass state is demonstrated to compare our model with the experimental results. We obtained a good agreement with the experimental results up to 0.3 meV (7%). To improve the stability of the trions (X −,   X +), in such structures, it is necessary to operate with a special QD size, which permits an enhancement of the binding energy.