The state of present technologies in technical and also non-technical practice is represented by growing complexity of systems. A turbojet engine as a complex system is multidimensional highly parametric system with complex dynamics and strong non-linear behavior with stochastic properties. Its particular property is operation in a wide spectrum of changes of its operating environment (e.g., temperatures from -60 to +40 °C, different humidity, different pressures, etc.). If we want to secure optimal function of such system, it is necessary to develop models and control systems implementing the newest knowledge from the areas of automation, control technologies preferably with elements of artificial intelligence (AI). The present control systems and dynamic models are often limited to control or modeling of a complex system in its certain (operational) states. However, in practice the turbojet engine finds itself in very different operating conditions that influence its parameters of operation and characteristics. To create progressive control algorithms for a turbojet engine, it is necessary to design models in the whole dynamic spectrum of the modeled system including its erroneous states. Furthermore we need to design a control system that will secure operation converging towards optimality in all eventual states of working environment and also inner states of the system represented by its parameters. This leads to the need of having increased intelligence of control of turbojet engines that reduces workload of a pilot and also increases safety of operation. Safety represents a decisive factor in design of control systems of turbojet engines and is presently bound with increasing authority of them. The present trend designates such control systems as FADEC – Full Authority Digital Engine Control, however in reality such control systems have different levels of authority, intelligence and come in very different implementations. These are often not presented as they are intellectual properties of commercial companies. The article will be aimed on description of some present trends in development of FADEC systems and own proposals of methodologies leading towards design and implementation of a FADEC system with high level of intelligence able to solve all operational situations of a turbojet engine. This is strictly bound with presentation of modern methods of modeling of turbojet engines and the use of advanced methods of mainly sub-symbolic artificial intelligence. The proposed methods are all tested in real-world environment using a small turbojet engine MPM-20 in our laboratory setup. Therefore the article will also deal with approaches in digital real-time measurement of state parameters of this engine and design of control algorithms from engineering standpoint.
Modern control systems of turbojet engines
The main global aim of control of turbojet engines is similar to other systems and that lies in increasing their safety and effectiveness by possible reduction of costs. This requires application of new technologies, materials and new conceptual solutions. One mean to achieve that is the development in systems of control and regulation of the engines themselves and processes ongoing in them.
Demands for control and regulation systems result mainly from specific properties of the object of control – a turbojet engine. The basic functions of control systems of a turbojet engine are the following ones – manual control, regulation of its parameters and their limitation. Manual control and therefore choice of regime of the engine is realized by a throttle lever according to a flight situation or expected maneuver. By regulation of a turbojet engine we understand such a kind of control where the chosen parameters of the engine are maintained on certain set levels, thus keeping its regime.In the past, the classical control systems of turbojet engines were implemented mainly by hydro-mechanical elements, which however suffered from deficiencies characteristic for such systems. Among such deficiencies were, high mass of such systems, inaccuracies due to mechanical looses and low count of regulated parameters. However development of electronic systems and their elements is ongoing, which will allow to increase precision of regulation of parameters of turbojet engines and their count to secure more complex and precise control of turbojets.
Use of electronics and digital technologies in control systems of turbojet engines has brought: (Lazar, 2000):
• lowering of mass of control system
• higher complexity of control – The count of regulated parameters used to be 3 to 7 by hydro-mechanical systems, however the digital systems operate with 12 to 16
parameters;
• increasing of static precision of regulation of different parameters (for example, precision of rotations from ±0.5 % to ±0.1 %, precision of regulation of temperature from
±12K to ±5K
• increase in reliability, service life and economics of operation of the driving unit of an aircraft;
• easier backup, technology of use and repairs, possibility of use of automatic diagnostics. By design of solution of a control system for a turbojet engine, it is necessary to build anappropriate mathematical model of the engine. The ideal approach to design of electronic systems is a modular one, from hardware or software point of view. This implies use of qualitative processing units that are resistant to noises of environment and also realization of bus systems with low delays is very important in this approach. Further improvement in quality of control can be achieved by implementation of progressive algorithms of control, diagnostics and planning in electronic systems. These algorithms have to be able to asses the state of the controlled system (turbojet engine in our case), then parameterize action elements and they have to be able to control the engine under erroneous conditions represented in outer environment or as errors in subsystems of the engine itself. Prediction of such states represents an area to incorporate predictive control system. Methods of situational control bound with elements of artificial intelligence supply many robust tools for solution of afore mentioned problems and sub-problems.
From the point of view of use of electrical and electronic systems in controls the turbojet control systems can be roughly hierarchically divided into following sets (Lazar, 2000):
1. Electronic limiters,
2. Partial Authority Flight Control Augmentation (PAFCA,
3. „High Integration Digital Electronic Control“ (HIDEC); „Digital Engine Control“ – (DEC); „Full Authority Digital Engine Control“ – (FADEC)). The division of control systems into these three levels is not absolutely distinct, as systems
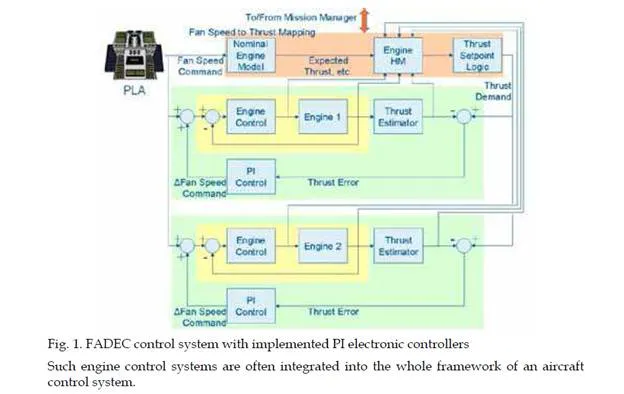
on higher level as for example HIDEC system can utilize control mechanisms as electronic limiters. For example FADEC systems are often realized as single or double loop control systems with utilization of PI control algorithms or electronic limiters with estimation filters (Jonathan, 2005; Sanjay, 2005). Example of such FADEC algorithm is shown in figure 1 (Jonathan, 2005).
Full authority control systems
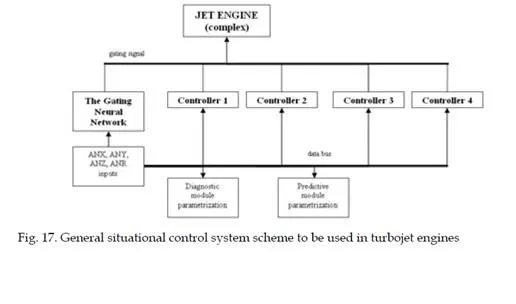
There are of course many possibilities and methodologies applicable to control systems of turbojet engines, which are FADEC compliant. Such application has to cope with strong non-linearity and changing structure of models and constants during operation of a turbojet engine. Such intelligent system should also be able to form decisions and predict faults either in control circuit or the object of turbojet engine itself. Therefore intelligent turbojet engine control is often bound with design of intelligent diagnostics systems (Wiseman, 2005) that also deal with control of an engine during its long-term deterioration. Example of such control based on diagnostics modules is shown in figure
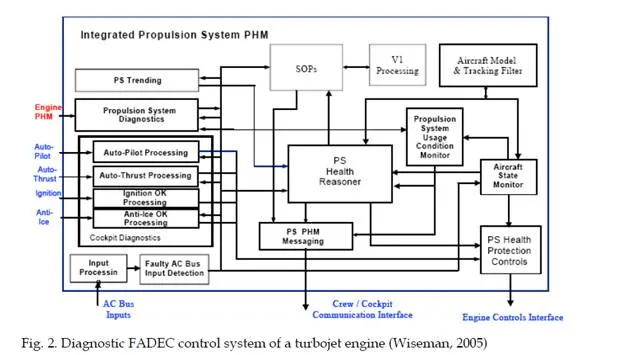
The control system in this case is based on intelligent PHM (Prognostics Health Management) of the engine. Diagnostic systems of turbojet engines can be further realized by means of artificial intelligence. In design of diagnostic and control system which would control the engine in its erroneous states and act long before actual critical states develops itself; we need to form exact dynamic models of the engine. In design of classic control systems only first to second order linear models are commonly used. Methods of AI however offer possibilities of modeling the dynamic parameters of an engine in multi variable space with great precision in the whole range of operation of engine. Such models can have precision within 2% of standard error in whole area of operation of a jet engine (Andoga, 2006). Integrated model used for control of a turbojet engine can be seen in figure
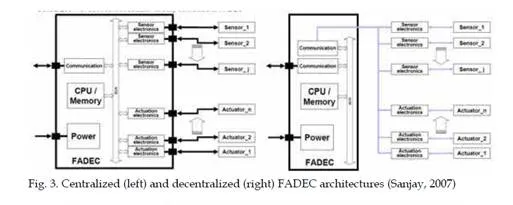
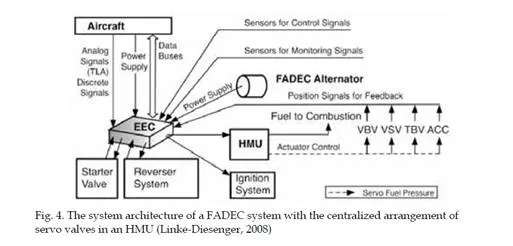
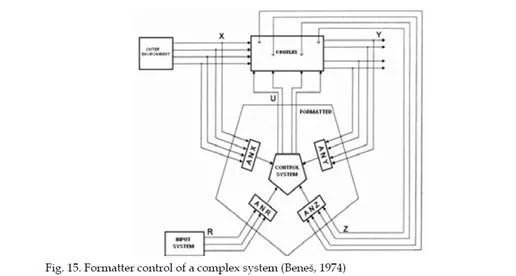
1. Importance of modeling during operation of a turbojet engine can be further extended to fault detection of sensors and other parts of control system and the engine itself. In design of control system, the architecture also plays a significant role. Two common architectures can be presently found in design of turbojet engine FADEC control systems (Sanjay, 2007). The first one is the centralized one, which is reliable and well understood, but on the other hand has many drawbacks like inflexibility, high weight, complicated fault detection, etc. This architecture is shown in the figure 3. The other usable architecture for design is the distributed architecture (fig. 4). Its main advantage is high flexibility, easier fault detection and isolation, its cons are mainly higher complexity, communication unknowns and deterministic behavior and it requires new technologies, i.e. high temperature electronics for use in turbojet engines. The basic element of the FADEC control system is the electronic engine control (EEC) unit that represents the main computer (outlined in black, in the previous figures). Such systems that are presently used to control common commercial airliners’ engines can be schematically depicted in the following figure 4 (Linke-Diesenger, 2008).
Small turbojet engine – MPM 20
The experimental engine MPM 20 has been derived from the TS – 20 engine, which is a turbo-starter turbo-shaft engine previously used for starting engines AL-7F and AL-21F. The engine has been rebuilt to a state, where it represents a single stream engine with radial compressor and a single stage non-cooled turbine and outlet jet. The basic scheme of the engine is shown in the figure 5
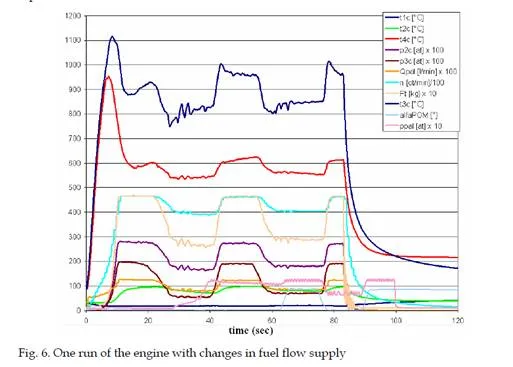
All sensors, except fuel flow and rotations sensor, are in fact analogue and have voltage output. This is then digitalized by a SCXI measurement system and corresponding A/D converters and sent through a bus into computer. Every parameter is measured at the sampling rate of 10 Hz. The data acquisition has been done in LabView environment. The digital measurement of parameters of MPM-20 engine in real time is important to create a model and control systems complying with FADEC definition („Full Authority Digital Electronic Engine Control“). Moreover we needed to change the engine from static single regime engine into a dynamic object, what was done by regulation of pressure beyond the compressor according to which the current fuel supply actuator changes actual fuel supply for the engine in real time. The system has been described in (Andoga, 2006). The graph in figure 6 shows dynamic changes of parameters of the engine to changes of fuel supply input.

Modeling of turbojet engines
Basic approaches in modeling of turbojet engines
In order to design and develop a control system for a turbojet engine, its mathematical model has to be constructed. In mathematical modeling of technical systems, many approaches can be used for different purposes. Specifically in the area of turbojet engines modeling two basic can be used. The first one is the analytic one that is usually developed under equilibrium conditions and uses physical relations and formulas to model usually static characteristics of different areas of an engine like inlet system, compressor, combustion chamber, etc. Such model is mainly used in design of the engine itself and to estimate basic operating parameters and envelopes in different environments. Basic control laws can be also estimated from such model. The second approach used mainly in design of control algorithms and diagnostic systems lies in creation of dynamic experimental models that model the engine or its parts as black boxes as transfer functions between input and output parameters (Harris, et. al, 2006). These models are aimed on simulation of dynamic behavior and regimes of an engine. To create a complex and intelligent control system both approaches have to be used and the further sections of this chapter will show some of these approaches to create precise computational models with use of elements of artificial intelligence. The authors of the paper deal with both approaches in modeling and as a real- world object a small turbojet engine MPM-20 is used.
Analytic modeling
Static and dynamic properties of turbojet engines (MPM-20) can also be described by a mathematical model of operation single stream engine under equilibrium or non- equilibrium conditions. This will allow modeling the thrust, fuel consumption, pressures and temperatures of the engine by different altitudes and velocities in the chosen cuts of the engine.
The steady operation of the engine is such a regime, where in every element of the engine same thermodynamic processes are realized. Operation of an engine in its steady operation can be described by:
1. algebraic equations of balance of mass flow of working materials through nodes of the engine, equations of output balance, equations of regulation rules and equations describing particular oddities of an engine. A system of equations expresses that for given outer conditions of operation of an engine, characteristics of all nodes of an engines and preset values of control parameters (fuel supply, cross section of the output nozzle, angle of compressor blades), operation of the engine will settle itself on one and only one regime (Ružek, Kmoch, 1979) .
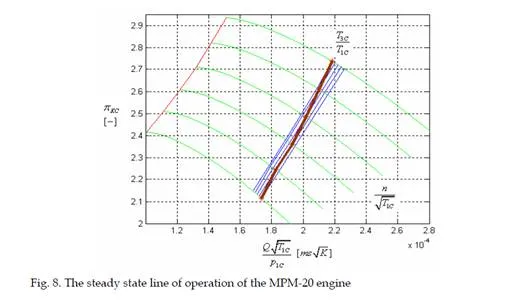
2. graphically by utilization of knowledge of characteristics of all parts (output, compressor, turbine, etc) of the engine and their preset curves of joint operations (e.g. lines of stable rations of T3c/T1c in compressor). Designation of all curves of the engine is done in a way that we will try to fulfill continuity conditions for all parts of the engine and characteristics of all these parts are given. These characteristics can be found by direct measurement, computation, etc.
Any regime of the turbojet engine has to fulfill the continuity equation which designates dependencies between mass flow of air through the compressor, turbine, combustion chamber and exhaust system (Považan, 1999):






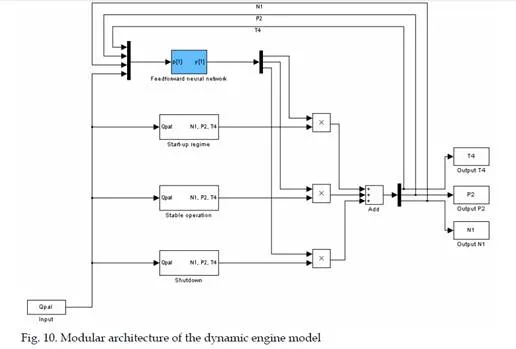

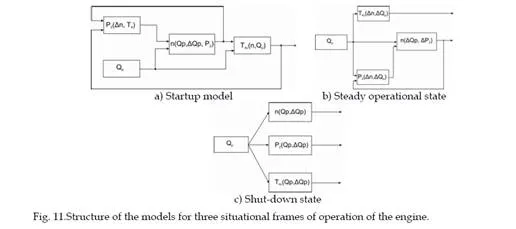
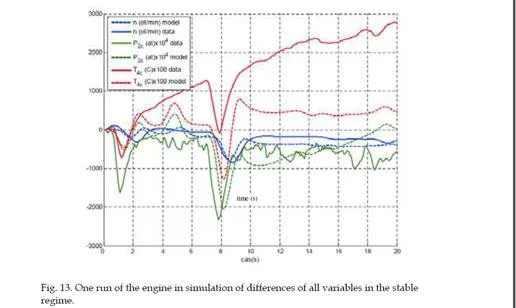
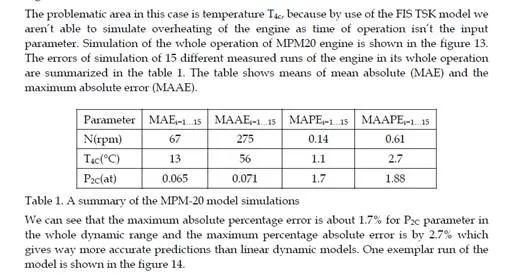
Situational control system design for a turbojet engine
Methods of artificial intelligence may offer new quality into control systems. However they can bring such benefits only after a careful model based analysis of a system where they should be applied with regards to simplicity and error free operation of such control system. Because on the lowest level of control we deal mostly with data and raw numbers, the approaches of sub-symbolic AI are appropriate to be used in design of intelligent FADEC control systems. However, on higher level of integration some symbolic concepts could also be used. From the area of symbolic AI three basic approaches can be successfully used:
• neural networks,
• fuzzy inference systems,
• genetic algorithms
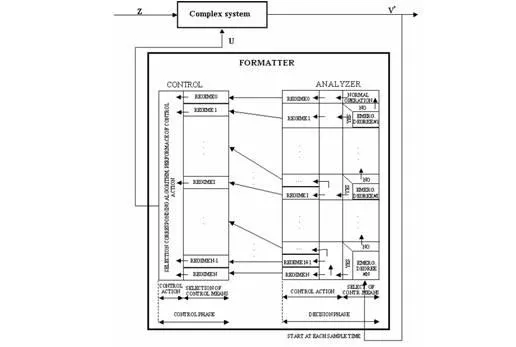



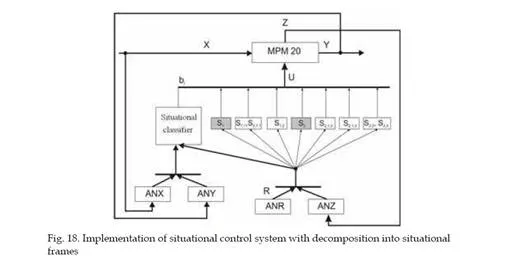
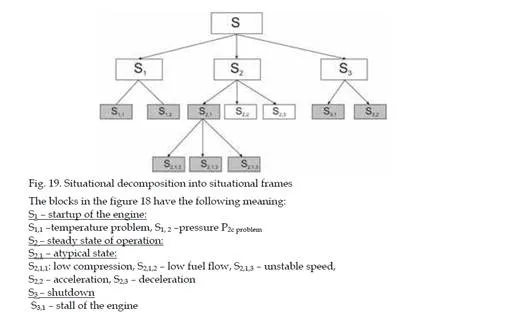
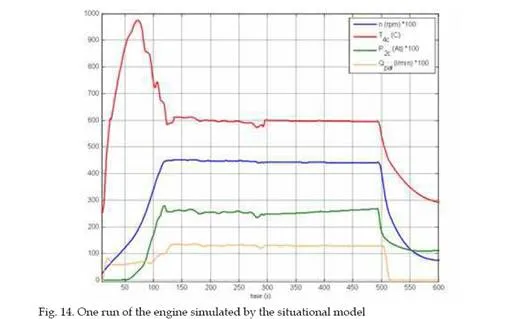
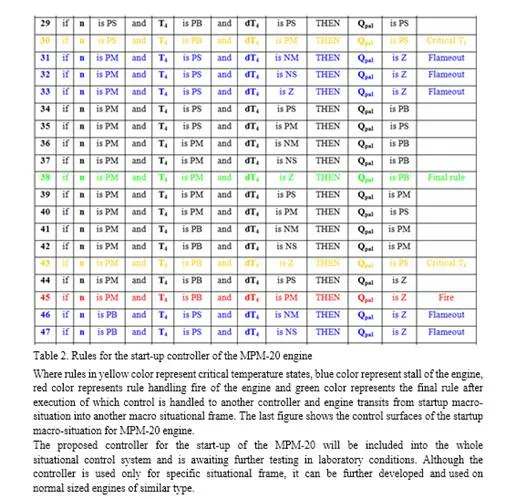
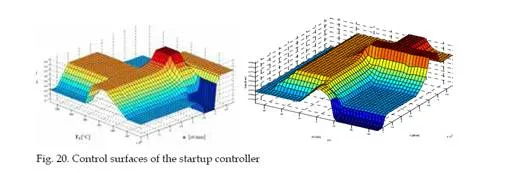
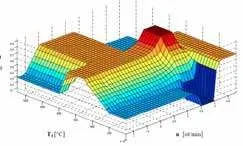
Start-up controller design for the MPM-20 engine
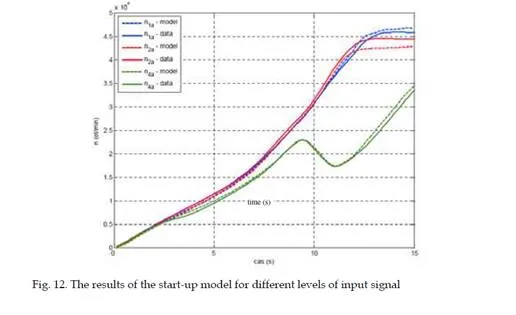
In design of control algorithms as elements of an integrated control circuit fuzzy inference systems can be successfully used. Such system has been used to design a startup controller for MPM 20 – the experimental small turbojet engine. This controller is acting only by startup of the engine and its aim is to decrease the temperature overshoot by startup that decreases life cycle of the engine and in certain cases can lead to turbine engine damage. The present startup techniques are mainly time based, what means that the fuel flow input is increased in a time based function rather than parameter based. The control algorithm can be seen as controller S1 in the figure 18 and is bound with digitally controlled servo vent for fuel supply control.The basic idea is to decompose the startup process of the engine into model micro- situational frames, where one rule of the inference system would correspond to one micro- situational frame in the start-up macro-situational frame. Each rule in the form of <IF> <THEN> postulate has a corresponding output value of fuel supply assigned. In this way we can handle not only the classical situations at startup, but also emergency situations like flameout of the engine or fire in the engine at startup. Three inputs and one output were chosen for the rules so the rule looks like this:

 Conclusion
Conclusion
The article presented some basic approaches in modeling and control of turbojet engines in general and applied for the object of the MPM-20 engine. This engine gives us an ideal test bed for research of methods in the areas of non-linear dynamic systems modeling and design of advanced control algorithms. Further research will be done in the area of situational modeling that will be headed towards broadening of input parameters of the situational model of the engine and further refinement situational classes. In this area we will be aimed at use of automatic algorithms to find boundaries between situational frames within multivariate space of parameters contrary to their setting by an expert. This also applies for situational control algorithm with the main aim lying in research of adaptive situational classifier systems that will be able to create classes and automatically assign controllers for them. All research in the areas of situational modeling, situational control should bring new quality of control and modeling in the area of turbojet engines and we expect this knowledge to be also expanded to other areas of technical systems.
The article presented some basic approaches in modeling and control of turbojet engines in general and applied for the object of the MPM-20 engine. This engine gives us an ideal test bed for research of methods in the areas of non-linear dynamic systems modeling and design of advanced control algorithms. Further research will be done in the area of situational modeling that will be headed towards broadening of input parameters of the situational model of the engine and further refinement situational classes. In this area we will be aimed at use of automatic algorithms to find boundaries between situational frames within multivariate space of parameters contrary to their setting by an expert. This also applies for situational control algorithm with the main aim lying in research of adaptive situational classifier systems that will be able to create classes and automatically assign controllers for them. All research in the areas of situational modeling, situational control should bring new quality of control and modeling in the area of turbojet engines and we expect this knowledge to be also expanded to other areas of technical systems.