Introduction
The Fourier law proposed in 1822 [1] is the fundamental of thermal conduction. It indicates that the heat flux passing through a material is proportional to the local gradient of temperature

here q is the heat flux, ∇T is the local temperature gradient, and κ is the thermal conductivity, which represents the material capability of transferring heat. In a long term, the Fourier law can accurately model the heat conduction. In the middle of twentieth century, theoretical physicists started to question the Fourier law because of its contradiction to the second law of thermodynamics [2]. After that, the heat waves were observed in low-temperature experiments [3] and aroused people’s interest as well as controversy. In 1980s, the short pulse laser experiment stimulated a lot of research and led to several relaxational [4], hyperbolic [5], or lagging types [6] of models, which can be regarded as the generalization of Fourier law. The above research focused on the distortion of ordinary heat transfer in short time scales. On the other hand, the shrink of space scales caused another type of distortion and began to be realized in the early 1990s, when sign of failure of Fourier law was perceived in thin dielectric films [7]. The phenomena of anomalous heat transfer in small scale materials can be fundamentally understood through the kinetic theory of phonons, that is, the thermal conductivity of dielectric materials can be formulated as [8, 9]

where C is the specific heat per unit volume, vv is the average group velocity of phonon, and λ is the phonon mean free path (MFP). When the material size is much larger than MFP, the MFP can be regarded as a constant and is dominated by the intrinsic phonon-phonon scattering and phonon-defect scattering rates. Therefore, the thermal conductivity is independent on the system size. In contrast, when the material size reduces to comparable value with the MFP, the phonon-boundary scattering becomes considerable. In this condition, the smaller system size induces higher boundary scattering rates and consequently shorter effective phonon MFP. By using Eq. (2) one figures out the reduction of thermal conductivity of nanomaterials.
The reduced thermal conductivity of nanofilms is a disadvantage for the heat dissipation in IC chips or semiconductor lasers. Nevertheless, it is an advantage for the thermoelectric devices. Experiments showed that the silicon nanowires have very high figure of merit (ZT) [10, 11]. The nanocomposites also demonstrate considerable ZT benefiting from the nano-sized superlattice or grains significantly scatter the phonons and reduce the effective thermal conductivity [12, 13]. Therefore, a lot of effort has been made to fabricate materials with ultra-low thermal conductivity through nanotechnology with the target at high ZT for the applications in advanced heating and cooling, waste heat recovery [14], as well as solar thermoelectric generators [15].
Due to the fast growth of energy-related nanomaterial synthesis and its transition from laboratory to industrial applications, modeling the thermal conducting behavior in nanosystems is in urgent need. Ideally, it should rise from a perspective of characterizing the fundamental physics and approach to simply structured theory which can be conveniently used by engineers. Nevertheless, this goal has not been satisfactorily achieved and current research is paving toward it. The gray model proposed by Majumdar is a pioneer work in this path. It predicts the effective thermal conductivity as [7]

where κeff is the effective thermal conductivity, κ0 is the thermal conductivity of the bulk material, L is the characteristic size of system, and β is a dimensionless parameter. Except that the temperature is much lower than the Debye temperature, the phonon scattering at most engineering surfaces can be regarded as diffusive. In this case, it was derived that for the in-plane heat conductivity of nanofilms, β= 3/8. For the cross-plane heat conductivity of nanofilms, β = 4/3. For the longitudinal heat conductivity of nanowires, β can be selected as 4/3 [16]. Kn is the Knudsen number, which is the ratio of MFP over L. Kn is actually a concept in gas dynamics, and it is well known that rarefaction effects should be considered in high Kn situations [17]. Eq. (3) was derived from an analogy between photons and phonons as wave packets of energy. Therefore, radiative transfer was assumed for phonons. It is easily found that Eq. (3) retreats to the Fourier law when the system size is much larger than MFP, that is, at the bulk limit. When the system size is comparable with the MFP, Eq. (3) delineates the size dependency of thermal conductivity. However, along with the progress in measuring the thermal conductivity of thin silicon films [18–21], the accuracy of Eq. (3) was questioned. It was claimed that the MFP of monocrystalline silicon should be around 300 nm to match the experiment results [19], while the value based on Eq. (2) is around 42 nm. Chen et al. [22–24] proposed that the phonon MFPs of single-crystal Si at room temperature should be 210–260 nm considering that the phonons of different frequencies contribute differently to the heat conduction. This amendment partly resolves the inaccuracy of gray model. However, it still exhibits considerable deviations to predict the experiment value of nanowires [25]. McGaughey et al. [16] developed a model which accounts the full dispersion relation and the directional dependent scattering chances with surfaces. This model matches well with experiments for nanofilms, while still overestimating the experiments for nanowires.
The phonon hydrodynamics [26–31] is another pathway to model the nanoscale heat conduction. It originates from the solving of linearized Boltzmann equation. An additional term representing the second order spatial derivative of heat flux, ∇2q, is involved in the governing equation of heat conduction. Since the heat flux is similar to a fluid flow flux, ∇2q is in analogy with the viscous dissipation term in Navier-Stokes equation for fluid mechanics. Therefore, the heat flux could be nonuniform in the heat transfer cross-section due to the drag from the boundary, forming a Poiseuille flow of heat. This behavior induces the terminology of “phonon hydrodynamics.” The analysis based on phonon hydrodynamics indicated the effective thermal conductivity of nanosystems should be inversely proportional to the square of Kn due to the nonuniform distribution of heat flux profile. However, the experiments indicated that the effective thermal conductivity is approximately linear to the characteristic size rather than the square of size. It is thereby further elucidated that the boundary velocity slip would happen in case of large Kn [29, 31]. By introducing the slip boundary condition into the governing equation, the linear size-dependent effective thermal conductivity can be achieved. The drawbacks of present phonon hydrodynamics analysis are: 1. The arbitrary in choosing the style and parameters of slip boundary condition. 2. The deviation from the physical picture of original derivation of Boltzmann equation, where it was the normal (N) scattering processes that induced the second order spatial derivative of heat flux. The present phonon hydrodynamic models just simply use the MFP of resistive (R) scattering processes as the parameter of ∇2q.
Upon the abovementioned progresses and their defects, the development of better models characterizing heat conducting in nanomaterials should base on capturing the essential feature of its physics. In recent years, the thermomass theory has been developed in our group, which proposes a mechanical analysis framework for heat transfer [32–35]. The generalized heat conduction governing equations are established based on such analysis. In the following sections, we will present the application of thermomass theory in nanomaterial heat conduction. The size dependency of thermal conductivity, thermal rectification, and thermoelectric effects will be addressed.
Thermomass theory
In history, the nature of heat was regarded as either a fluid, that is, caloric theory. The caloric theory regards heat as a weightless, self-repulsive fluid. In the eighteenth and the first half of nineteenth centuries, the caloric theory was the mainstream theory. It was extinct after the mid-nineteenth century and replaced by the dynamic theory that the nature of heat is the random motion of particles in a body. In twentieth century, Einstein’s relativity theory introduced the well-known mass-energy equivalence relation, E = mc2, where c is the speed of light. According to this theory, the thermal energy should correspond to a certain amount of mass. To illustrate his theory, Einstein elucidated “a piece of iron weighs more when red hot than when cool” [36], which means the adding of the thermal energy into material, that is, raise its temperature and at the same time increase the mass. The mass increase induced by heat was defined as “thermomass,” which is very small in ordinary conditions. For example, the thermomass of Si at room temperature is 10−12 of the total mass. Such small amount of mass is negligible when dealing with the dynamic problem, like movement and balance of the body. However, the heat conduction is the movement of thermomass itself relative to molecular or the lattice. It is driven by the pressure gradient induced by the concentration difference of thermomass among the materials. The forces and inertia of thermomass are comparable and lead to the limited acceleration and drift velocity of it. The advantage to bring in the concept of thermomass is that the analysis of heat conduction can follow a mechanical framework. The corresponding forces, velocities, accelerations, and momentums can be properly defined.
Consider the dielectric solids, the phonons are the main heat carriers. In this case, the internal energy per unit volume, e, is the summation of all phonon energies [9]

where ħ is the reduced Planck constant (Dirac constant), ω is the phonon frequency, k is the wave vector, and n denotes the index of phonon branches. f is the phonon distribution function. In equilibrium state, f obeys the Bose-Einstein distribution

where kB is the Boltzmann constant. The density of the thermomass, that is, the equivalent mass of the phonon gas, is obtained by using the Einstein’s mass-energy equivalence relation

It should be reminded that the frequently used expression for thermal conductivity of phonon systems, Eq. (2), is from the analogy between gas and heat carriers. The scattering of phonons induces resistance on heat transport. Generally, the scattering accounted for thermal resistance is the R processes, including the Umklapp scattering, defect scattering, and boundary scattering. These scattering events eliminate the quasi-momentum of phonons. The MFP defined in Eq. (2) refers to the traveled distance of a phonon between succeeding R scatterings. However, in ideal gas systems, the collision among gas molecules does not perish the momentums. Therefore, the R processes of phonons are more resemble to the collision of gas molecules to residential barriers. It is the case when a gas flows through a porous medium. The collision frequency between gas molecules and material skeleton determines the resistance experienced by the gas flow. In the porous flow, the Darcy’s law describes the effective flow velocity is proportional to the pressure gradient

The pressure gradient can be regarded as the driving force of flow. From a viewpoint of force balance, the driving force is actually balanced by the friction force. Thereby Eq. (7) essentially depicts that the friction force is proportional to the flow velocity. It is a general case in laminar flow.
In analogy to the gas flow in porous medium, the velocity of thermomass is defined as

The mass and momentum balance equations of thermomass can be derived as [32–34]
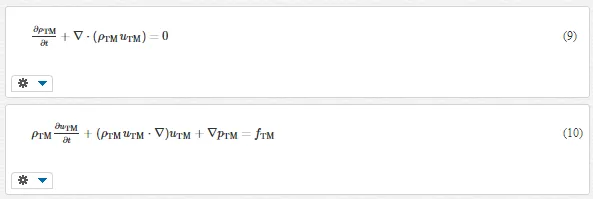
where pTM is the phonon gas pressure, and fTM is the friction force impeding the phonon gas. Eq. (9)gives the energy conservation equation by applying Eqs. (6) and (8). Eq. (10) characterizes the heat transport, which is the motion of thermomass through the materials. To obtain the explicit heat transport governing equation, the pressure and friction terms need to be determined. If the phonons are viewed as moving particles with finite mass, the pressure of them can be derived by accounting the momentum change when these particles hit and rebound from a unit area of the container surface, in analogy to the kinetic theory of gas. In a result, the pressure of phonon gas can be expressed as

where vvg is the group velocity of phonons. For bulk material, the friction experienced by thermomass can be extracted from Eq. (7). When discussing the nanosystems, the boundary effect needs to be considered. The Darcy’s law for porous flow was extended to Darcy-Brinkman relation when the boundary effect is nonnegligible [37, 38]

here μ is the viscosity, K is the permeability with a unit of m2. Eq. (12) indicates that the boundary slip velocity attenuates from the boundary with a characteristic length of K1/2 to the uniform velocity in the porous medium. The introducing of a second-order spatial derivative term also makes Eq. (12) the same order as the governing equations for free flow. In the steady flow, the driving force is balanced with the friction force. Following the form of Eq. (12), when the boundary effect is considered, the friction of thermomass can be formulated as

where χ is the friction factor. The permeability of the thermomass in heat conducting medium is

In large systems, the boundary effect is negligible. Then, Eq. (13) reduces to the Darcy’s law with the first term much more important than the second term on the right hand side.
When the spatial gradient and changing rate of physical quantities are not significant, the first and second terms in Eq. (10) can be neglected. In this case, Eq. (10) exhibits the balance between driving force and friction force. The heat conduction is steady in such a nonequilibrium system. Combining Eqs. (13) and (10) leads to

For the simplest case, vvg and C are assumed to be temperature independent. Then, Eq. (15) actually gives the Fourier law with

When the boundary effect is considerable, the second term in Eq. (13) needs to be accounted. In this case, the combination of Eqs. (13) and (10) gives

where lB equaling to the square root of KTM is a characteristic length.
Eq. (17) is a generalization of Fourier law when boundary effect needs to be considered. It predicts the reduction of effective thermal conductivity in nanosystems by the additional resistance term. When the system size is bigger, the spatial gradient of q is smaller. Thus, κeff increases with the system size growing larger. Nevertheless, to quantitatively predict the size dependency of κeff and compare it with experiments, the exact value of lB needs to be determined for certain material. The thermal conductivity is a macroscopic physical quantity, which is usually obtained by experiments. Similarly, with plenty of experimental data, the value of thermomass permeability and lB could be evaluated. However, nowadays the experiments in nanosystems are still expensive and have large uncertainty. Therefore, in the following, a bottom-up strategy, namely, raising from microscopic phonon properties, is used to extract the value of lB.
Phonon Boltzmann derivation
For dielectric solids, the Boltzmann equation describes the evolution of phonon density of state as in Ref. [26, 27]

where D is the drift operator and C is the collision operator. Eq. (18) indicates that the phonon gas can freely drift without the disturbance of collision. The drift operator is

where vvk is the phonon velocity in one Cartesian direction. The collision, such as the phonon-phonon scattering, reshapes the phonon distribution function. In phonon theory, the collisions can be sorted to R and N processes. The R processes break the phonon quasi-momentum, while the N processes conserve it. In this sense, the collision operator can be simply formulated as

where τR and τN are the characteristic relaxation time between succeeding R and N events. f0 is the equilibrium distribution given by Eq. (5), fD is the displaced distribution

where uD is the drift velocity of phonon gas. Eq. (20) illustrates that the R processes tend to bring f back to f0, while N processes tend to bring f to fD.
If f can be approximated with fD, a solution of Eq. (20) can be obtained with a second-order Taylor expansion of fD around f0 and then integrating [33]

If the friction force in Eq. (10) only has the first term, which is linear to the thermomass velocity, Eq. (22) is identical to Eq. (10) except the coefficient 15/16 in ahead of the second term on the left hand side. This difference is caused by the Doppler Effect during the drift motion of phonon gas. From this perspective, the phonon gas is slightly different from the real gas. The phonon energy varies due to the dispersion, causing the “eclipse” of the convection term. In a nondispersive medium, the frequency is independent of k. Then, Eq. (22) is consistent with Eq. (10). Nevertheless, the second-order spatial derivative term, like in Eq. (17), is dismissed. In nanosystems, the boundary condition should be considered in solving Eq. (18). For example, if the boundary is completely diffusive, the drift velocity in Eq. (21) is dragged to zero. In this case, the phonon distribution function is assumed to have the following form.

It indicates that with the diffusive boundary, the N processes induce a deviation from fD, with the relaxation length λN = vvgτN, i.e., the MFP of N processes. The additional term in Eq. (23) gives a second-order spatial derivative term. By the integration of Eq. (18), one gets
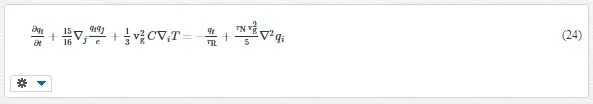

Eq. (25) can be regarded as the first order Chapman-Enskog expansion [17] of the phonon distribution function. In fluid mechanics, the viscous term in Navier-Stokes equation can be derived from the first order Chapman-Enskog expansion of the state distribution function of fluid molecular. Without the Chapman-Enskog expansion, the solution of Boltzmann equation gives the Euler equation, which is the dynamic equation without the viscous dissipation. This case happens when the interested region is far away from the boundary, or the boundary layer thickness is negligible compared with the flow region, like the large Reynolds number flow around the aircrafts. The difference between the thermomass flow and ordinary gas flow is that the R processes causes residential friction forces to the flow, which makes the transfer diffusive. In low temperature crystals, or low dimensional materials, such as graphene, the R processes can be rare. Then the heat conduction will exhibit obvious hydrodynamic behaviors. Therefore, based on the phonon Boltzmann derivation, the value of lB in Eq. (17) can be determined as lB2 = λRλN/5.
Phonon gas flo w in Si nanosystemsBased
on Eq. (25) we can calculate the effective thermal conductivity of nanosystems. The silicon nanofilms and nanowires are investigated here because the experimental results are available for comparison. The geometries of nanofilms and nanowires are shown in Figure 1. The direction of heat conduction is in-plane for nanofilms and longitudinal for nanowires.
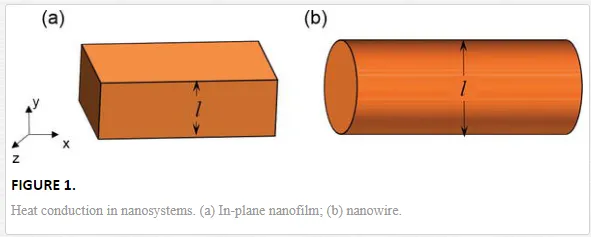
Assume the boundary is completely diffusive, i.e., the phonon gas drift velocity is zero on the boundary. The solution of Eq. (25) for a nanofilm is [39]
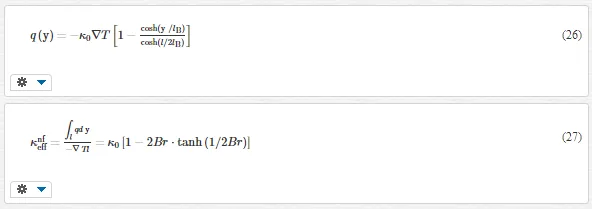
where l is the thickness of film and Br = lB/l is the Brinkman number. The solution for nanowire is
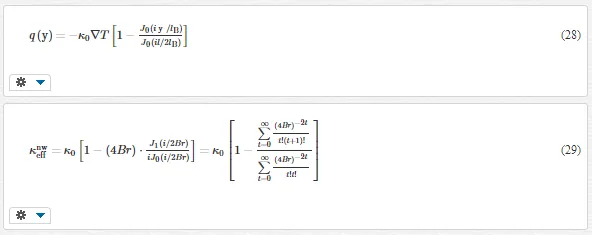
where l is the diameter (thickness) of the wire and J is the cylindrical Bessel function

Eqs. (26) and (28) show the heat flux is nonuniform at the cross-section. If the system size is much larger than lB, q(y) tends to be constant. Then, the effective thermal conductivity renders the bulk limit, κ0. If the system size is comparable with lB, q(y) is significantly affected by the boundary. Thereby, κeffis strongly reduced.
The analytical derivation of Eqs. (26)–(30) is based on the assumption that the lB is constant. However, in nanosystems, the phonon would scatter with boundary, which shortens the MFPs. For the pure diffusive boundary, the scattering on boundary will terminate the MFPs. It can be seen as the additional collision event into the ordinary scatterings. If the boundary is located at r away from the originating point, the effective MFP of phonons can be expressed as

In this way, the effective MFPs in nanosystems can be obtained by integrating over the sphere angle. For nanofilms, the local value of MFPs is [40]
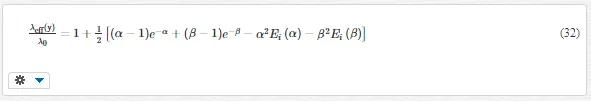
where α = (l/2−y)/λ0, β = (l/2+y)/λ0, and Ei(x)=∫∞1t−1e−txdtEix=∫1∞t-1e-txdt. For nanowires, we have
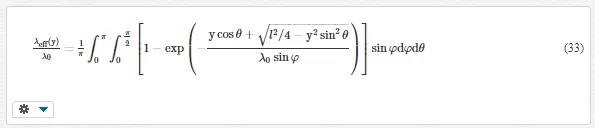
Therefore, the MFPs are significantly shortened in nanosystems. It reveals that the boundary has dual effects on heat conduction in nanosystems. First, the second spatial derivative of heat flux, which represents the viscous effect of phonon gas, imposes additional resistance on heat transfer due to the nonslip boundary condition. Second, the collision on boundary changes the effective MFPs. This effect is similar to the rarefaction of gas flow in high Kn case. By accounting both the dual effects, the thermal conduction in nanosystems is described as

It is worth noting that in fluid mechanics, the rarefaction is not necessarily happened at the same time of viscous effect based on the Darcy-Brinkman relation. Consider the water flow in porous material. The permeability of porous flow is determined by the size of pores, which typically is in the order of micrometers. The MFP among water molecule is typically subnanometer. Therefore, the square root of permeability differs much from the MFP. The effects of Darcy-Brinkman boundary layer and rarefaction can be unconjugated. On the other hand, if the fluid is replaced by gas, the MFP of fluid could be comparable to the square root of permeability. In this case, the Darcy-Brinkman boundary layer and the rarefaction should be considered simultaneously. For the phonon gas flow, the relative magnitude of λR, λN, and l decides the conjugation of boundary layer and rarefaction. λR represents the “size of pores” while λN represents the viscosity of phonon gas. The bulk limit is achieved when l >> λR and l >> λN. If λR >> l >> λN, the first term on the right hand side of Eq. (34) is less important than the second term. The flow mimics a dense fluid passing through a sparse medium. The boundary transmits momentum efficiently across the flow region. The phonon hydrodynamics can be observed. If λN >> l >> λR, the flow mimics a dilute fluid passing through a dense medium. The velocity profile will be close to linear. In this case, only the rarefaction effect needs to be considered. If λN >> l and λR >> l, both the rarefaction and boundary drag affect the resistance on flow and need to be modeled simultaneously.
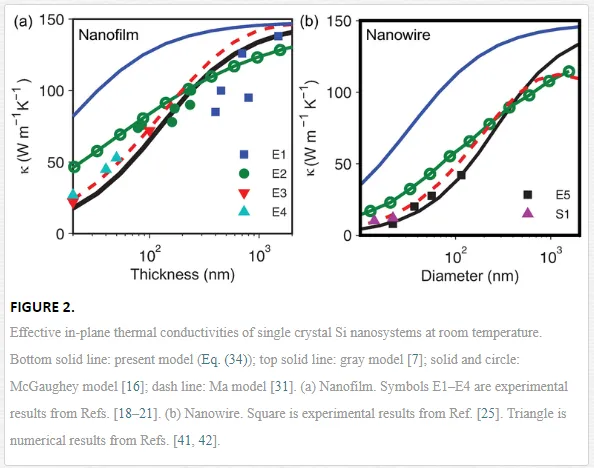
The numerical solution of Eq. (34) gives the effective thermal conductivity for Si nanofilms and nanowires at room temperature, as shown in Figure 2. The physical properties are adopted as κ0 = 148W/(m K) (standard experiment value for monocrystalline Si), λR,0 = 42 nm (according to the direct calculation based on Eq. (2)), λN,0 = 360 nm. The predictions based on the gray model [7], McGaughey model [16], and Ma model [31] are also presented in Figure 2. It shows the gray model and McGaughey model overestimate the thermal conductivities. Ma model gives close results to experiments. However, Ma model assumes a MFP of 210 nm, which is lack of physical support. It also shows an unreasonable drop at D = 1000–2000 nm for nanowires. According to Figure 2, our model achieves the best agreement with current available experiment and numerical results
Thermal rectification in nanosystems
Thermal rectification refers that the heat conduction in one direction of the device leads to higher heat flux than following the opposite direction, even though the same temperature difference is applied. It currently raises much interest since the first experimental report by carbon nanotubes [43]. The thermal rectification effect is anticipated to realize thermal diode [44], thermal logic gate [45], or thermal transistors [46, 47]. Though much effort has been paid for searching useful mechanisms and realizing considerable rectification ratio, the ambitious goal that controlling heat as electricity is still far away [48].
The mechanism of thermal rectification has been widely studied. It is found that various effects can induce rectification, such as the different temperature dependences of the thermal conductivity at the different parts of the device [49], the asymmetric transmission rates of phonons across the interfaces [50], and the temperature dependence of electromagnetic resonances [51]. Here, another rectification mechanism is proposed through the thermomass theory, following an analogy to fluid mechanics. In Navier-Stokes equations, the convective acceleration term indicates when the fluid experiences speed up or slow down. Therefore, if the cross-section area of a flow channel is changing (e.g. the trapezoidal channel), the flow rate under the same pressure difference is different in the convergent direction or in the divergent direction. In the convergent direction, the channel serves as a nozzle, which accelerates the fluid and converts part of its potential energy to the kinetic energy. In the divergent direction, the channel serves as a diffuser, which decelerates the fluid and converts part of its kinetic energy to the potential energy. The acceleration of fluid increases the velocity head and consumes the dynamic head of flow. Therefore, the total fluid flux in the convergent direction will be less than that in the divergent direction. In terms of thermal conduction, it means that with the same temperature difference between the heat source and sink, the total heat flux in the wide-to-narrow direction is smaller than that in the narrow-to-wide direction, which is the thermal rectification. Nevertheless, it should be stressed that for a flow channel with large angle of divergence, the flow separation could happen when the fluid velocity is high. In case of flow separation, the effective resistance of the diffuser will be much increased. It may cause the total heat flux in the wide-to-narrow direction larger than that in the narrow-to-wide direction, that is, the reverse of rectification.
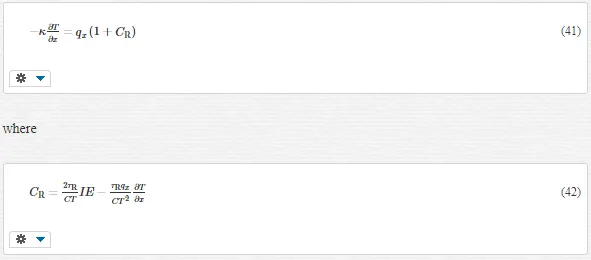
In steady state, the generalized conduction law, Eq. (10), can be reformulated as

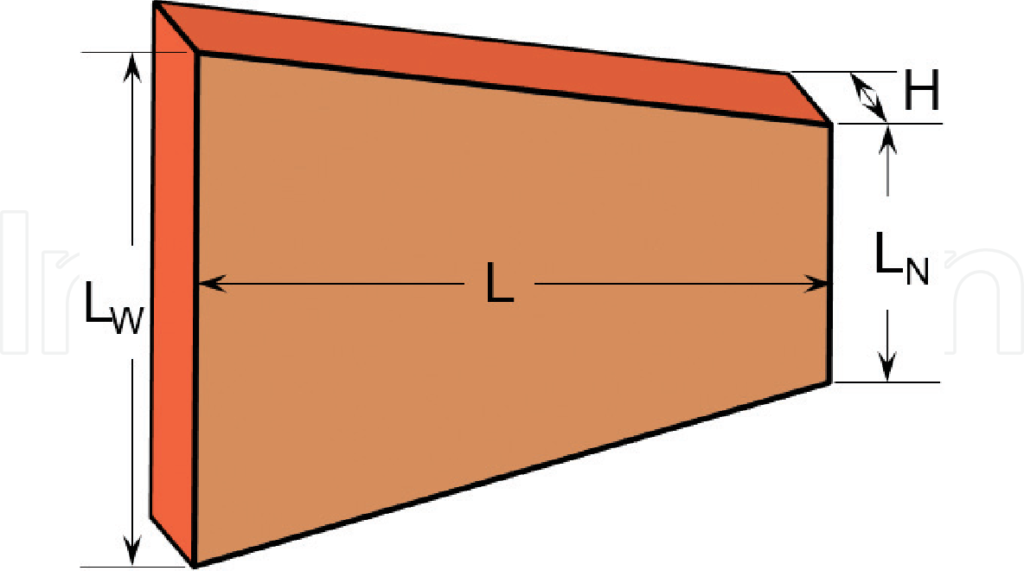
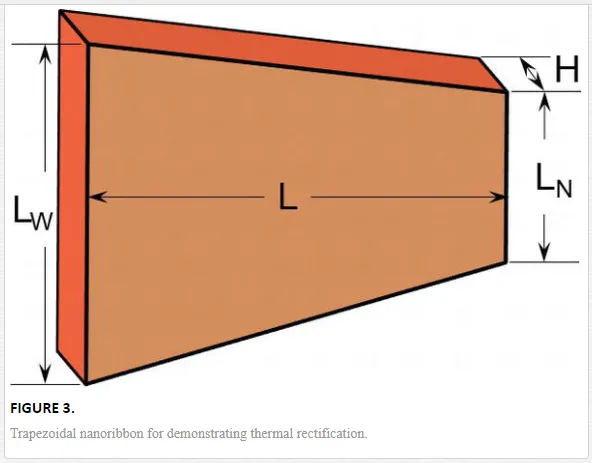
The difference between Eqs. (35) and (25) is the additional convective term, −τR∇jqiqj/e. The first term on the left hand side mimics to the spatial inertia term in fluid mechanics. It induces rectification effect. Consider a trapezoidal material with heat conducting through the symmetry axis, as shown in Figure 3. The thickness of the material is H; the widths at the narrow and the wide ends are LW and LN, respectively, and the separation between these ends is L. If L is much larger than LN and LW, the heat conduction can be assumed as quasi-one-dimensional. The mainstream of heat flux is in the x direction, qx >> qy. The total heat flux (Q) at each cross-section perpendicular to x direction is constant. Due to the boundary friction, the Laplacian of qx in the y direction is much larger than in the x direction. Then, the x component of Eq. (35) is
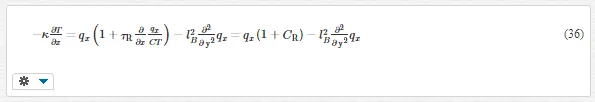
where CR consists of two terms

The sign of the first term of CR will be positive for the heat conduction in a convergent channel, which means the acceleration of heat flux creates additional effective resistance, and reduces the total heat flux. Oppositely, heat conduction in a divergent channel will increase the total heat flux. The second term of CR will not change sign with the direction of heat transport. It characterizes the acceleration due to density variation since thermomass is compressible. It is insignificant except for the case of ultra-high heat flux [52].
To enhance the thermal rectification, the directional sensitive part in Eq. (36) should be amplified over the directional non-sensitive part. If the diffusive boundary condition is replaced with slip boundary condition, or the system size is large compared with the boundary layer, the Laplacian term of heat flux can be neglected. In room temperature, the second term of CR is usually much less than the first term. In this case, Eq. (36) can be simplified to

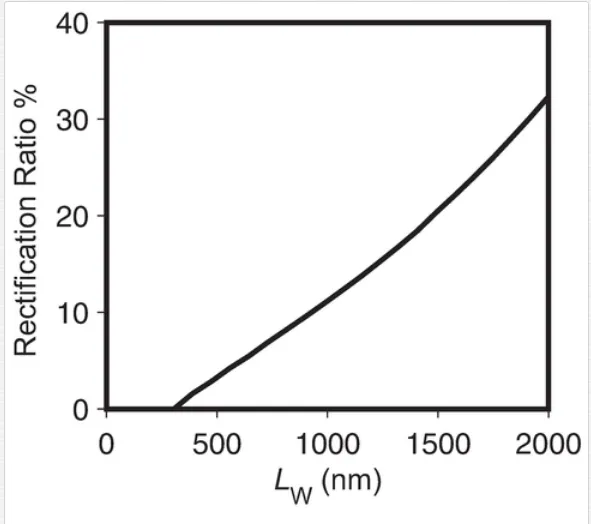
Consider a silicon ribbon with the average temperature 300 K. Assume that H = 1000 nm, L = 300 nm, LN = 300 nm, Lw varies from 300 to 2000 nm. The relaxation time τR is set as 1.5e−10s based on experimental results [53]. The temperatures on both ends are 330 and 270 K, respectively. By numerically solving Eq. (38), we can get the rectification ratio (defined as the thermal conductance in narrow-to-wide direction over that in the opposite direction), as shown in Figure 4. It shows that the rectification ratio grows with Lw, from zero to a considerable value of 32.3%. This value is large enough to construct thermal diode or thermal logic gate.
Thermoelectricity of nanosystems
The ZT for nanomaterials could be much enhanced [10–13]. The mechanism of such enhancement can be that the nanostructures reduce the thermal conductivity by strong phonon-boundary scattering while maintaining the electrical conductivity. Although a lot of work has been done in searching high ZT materials through nanotechnology, the thermodynamic analysis and the role of nonlocal and nonlinear transports, which are highly possible to happen in nanosystems, are not fully discussed [54, 55]. In recent years, the nonlocal effects raised by the MFP reduction due to geometry constraint [56], the electron and phonon temperature [57], and the breakdown of Onsager reciprocal relation (ORR) [58, 59] in nanosystems have been investigated from the framework of extended irreversible thermodynamics (EIT). These works showed that the nonlinear and nonlocal effects influence the efficiency of devices. The breakdown of ORR not only possesses theoretical importance but also shed light on approaches to further increase efficiency.
Here, we analyze the thermoelectric effect from the thermomass theory perspective. There could be various effects when the individual motion of phonon gas and electron gas is separately considered. The most apparent one is the energy exchange between phonons and electrons [60]. In a one-dimensional thermoelectric medium, the conservation of energy gives

where I is the electrical current and E is the electrical field. IE equals the adding or subtracting rate of thermal energy. Dividing Eq. (39) by c2 illustrates that the electrical current performs as the mass source or sink of thermomass. The nonconservation of mass brings additional term in Eq. (10). In steady state, we obtain the governing equation of thermomass momentum as

The second term on the left hand side is nonzero because of the energy conversion. It increases the spatial inertia of thermomass. For simplicity, we do not consider the Brinkman extension of the friction force and assume the material cross-section is constant, and then Eq. (40) turns to
Compared with Eq. (37), the first term of CR has a coefficient 2 because of the energy exchange between phonons and electrons. The electrical current couples with the heat flux and induces additional spatial acceleration force on the thermomass flow. This inertia increase is insignificant in ordinary conditions due to the small value of τR. It could be considerable in case of strong power thermoelectric convertor with large electrical current and intense electrical field. Neglecting the second term of CR, it can be derived that the effective thermal conductivity and Seebeck coefficient change to
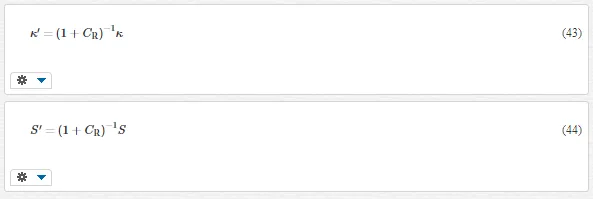
Since ZT is S2σ/κT, the effective ZT is (1 + CR)−1 of the original one without considering the inertia effect of thermomass. Therefore, when IE > 0, the electrical energy converts to thermal energy. It is typically the case of thermoelectric cooler. The heat flux is additionally impeded. The ZT is decreased. When IE < 0, the temperature gradient drives electric current. It is typically a thermoelectric generator. The heat flux is further pumped, and the effective ZT is enhanced. The inertia effect could be beneficial for a higher ZT of the device in this case.
Conclusion
In this chapter, we present a mechanical analysis on the thermal conduction in nanosystems with the thermomass theory. Firstly, the boundary resistance in nanosystems on heat flow is modeled with the Darcy-Brinkman analogy. The permeability of thermomass in materials is derived based on the phonon Boltzmann equation. The size-dependent effective thermal conductivity of Si nanosystems thereby is accurately predicted with the present model. Then, the spatial inertia effect of thermomass is shown to induce the thermal rectification in asymmetry nanosystems. The predicted rectification ratio can be as high as 32.3% in a trapezoidal Si nanoribbon. Finally, the energy conversion in thermoelectric devices can be coupled with the spatial inertia of thermomass flow. The ZT tends to be increased in case of a thermoelectric generator.