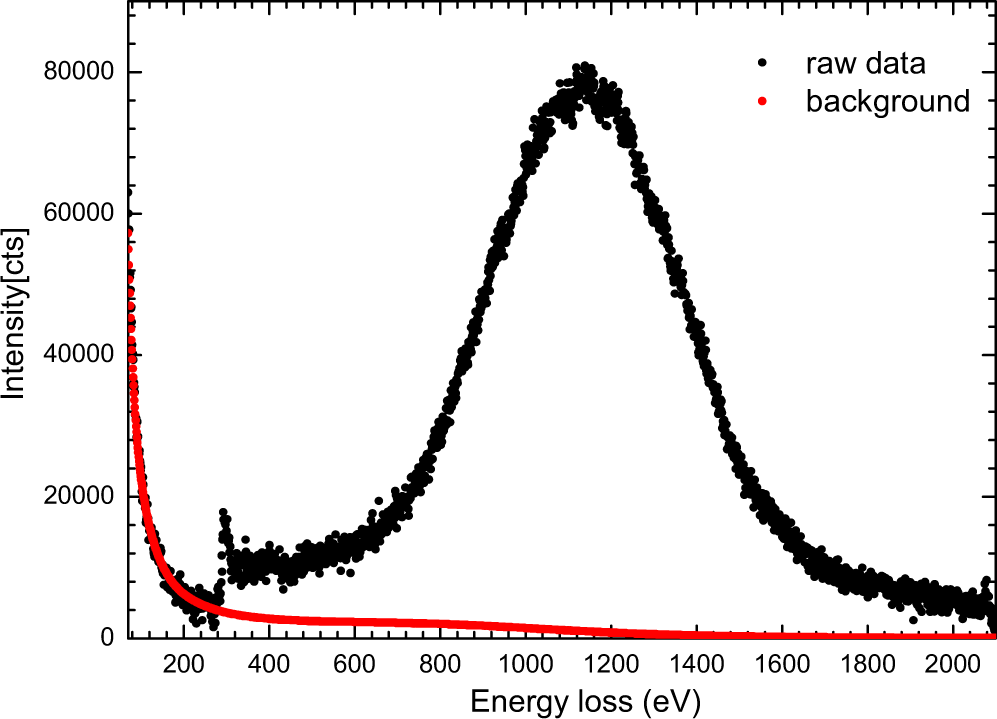
The Compton effectis the light-particle interaction where the wavelength of scattered photon is changed. The difference between
The Compton effect and the E instein photo effect consists in the fact that during the photo effect,the energy of photon is transmitted to electrontotally.Compton used in his original experiment[1] the energy of the X-ray photon(∼20keV) which was verymuch larger than the binding energy of the atomic electron, so the electrons could be treated as being free. Compton scattering usually refers to the inter action involving only the electrons of anatom. However, the nuclear Compton effect was confirmed too.The effect is important because it demonstrates that light cannot be explained purely as a wave phenomenon. The Compton experiment proved that lightis composed of particle-like objects with energy E=h¯ω. The interaction between electrons and high-energy photons is such that the electron takes part of the photon initial energy, and a photon containing there maining energy is emitted in a different direction from the original. If the scattered photon still has enough energyleft, the process may be repeated. Compton, in his paper[1], derived a simple formula relating the shift of wavelength to the scattering angle of the X-rays by postulating that each scattered X-ray photon interacted with only one electron. His paper involves the information on experiments for verification of the equation:


Graphene
Graphene is a two-dimensional carbon sheet which is very consistent(100 times stronger than steel). It is a verygood conductor of heat and electricity. Graphene was investigated by theorists for decades; however,it was first generated in the laboratory in 2003. Being two-dimensional, it interacts in a special way with light and with other materials. Researchers have discovered the bipolar transistor effect, the charge stictransport ,and the large quantu moscillations.Technically, grapheme is a crystal line allotrope of carbon with two-dimensional geometrical properties. Morethan 70 years ago, Peierls[3] and L andau[4]proved that the two-dimensional crystal is not stable from the view point of ther mody namics and cannot exist. The ther mody namic displacements of atoms in such a crystal are of the same sizeas the distances between atoms at any finite temperature. Mermin[5] accepted the theoretical argument sin1968,and it seemed that many experimental observations were in accord with the Landau-Peierls-Mermin theory. However, in 2004, Geim and Novoselov[6],[7]with co-workers at the University of Manchester in England produced a crystal line sheet of carbon just one-atom thick. Then,
The Geim group was able to isolate graphene and was able to visualize the new crystal medium using a simple optical microscope.The Landau-Peierls-Mermin proof remained as the historical document. After sometime, the new sophisticated methods generating grapheme sheets were invented. The grapheme sheets were, e.g., synthesized bypassing liquid than old roplets into an argon plasma. The authors of this method are Datoetal.[8]. Graphene is composed of the benzenerings (C6H6)without their H-atoms. Grapheneisonly one of the crystal line forms of carbon which crystal lizeas diamond,graphite,fullerene(C60), carbon nano tube,and glassy carbon. Unique physical properties of grapheme are caused by the collective behavior of the quasi particles called pseudo electron shaving pseudo pins, which move according to the Dirac equation in the hexagonallattice. Strong interactions between the electrons and the carbon atoms result in linear dispersion relationE=vF|p|,wherevFis theso-called Fermi-Diracvelocity, pbeing the momentum of apseudo electron.The Fermi velocity is approximately only about 300times lessthan the speed of light. The pseudo spin of the pseudo electron follows from the hexagonal form of graphene. Every hexagonal cell system is composed of the systems of two equilateral triangles. The fermions in the triangle sub-lattice systems can be described by the wave functionsϕ1andϕ2. Then the adequate wavefunction of the fermion moving in the hexagonal structure is their super position, orψ=c1ϕ1+c2ϕ2, where c1 and c2 are functions of coordinate x and functionsϕ1,ϕ2 are functions of the wave vector k and coordinate x. The crucial step in grapheme theory is the definition of the bispinor function with components ϕ1,ϕ2[9].
The relativistic generalization of non relativistic equation E=vF|p|is evidently the Dirac-Weyl equation for the description of neutrino which can be transcribed in four-components pin or form as