The forces known as buoyancy, drag, and lift arise when fluids interact with a solid structure or vehicle. Drag and lift forces arise when there is relative motion between a fluid and a solid object. A vehicle can either move through the fluid (as an aircraft moves through air,for instance) or the fluid can flow around the structure (such as a gust of wind impinging on a skyscraper). However, forces between fluids and solid objects can arise even if there is no relative motion.

What is Buoyancy Force

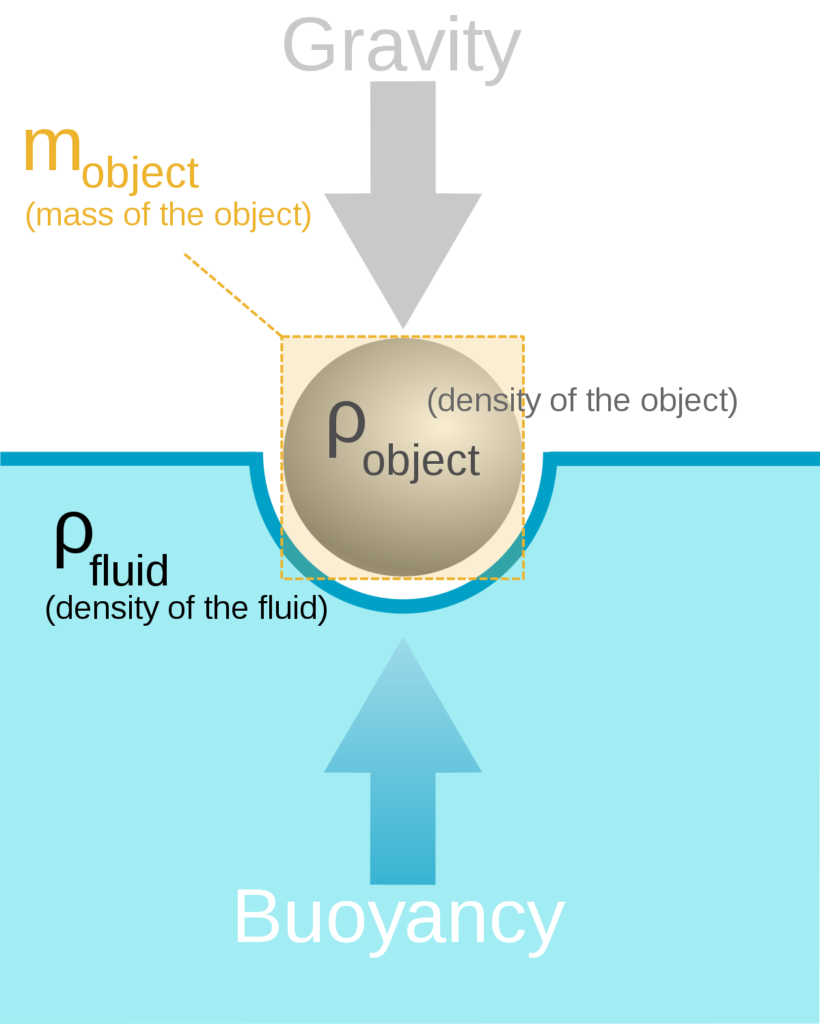
The force that develops when an object is simply immersed in a fluid is called buoyancy, and it is related to the weight of the fluid displaced.The weight of a quantity of fluid is determined by its density  (the lowercase Greek character rho) and volume. Table 1 lists the density values of several gases and liquids in the SI and USCS. The weight of a volume V of fluid is given by the expression –

w = ρgV

Table 1 : Density and Viscosity Values for Several Gases and Liquids at Room Temperature and Pressure

where g is the gravitational acceleration constant of 9.81 m/s^2 or 32.2 ft/s^2.For this equation to be dimensionally consistent in the USCS,  must have the units of slugs (not pound-mass) per unit volume.As you swim to the bottom of a pool or travel in the mountains, the pressure changes in the water or air that surrounds you, and your ears “pop” as they adjust to the rising or falling pressure. Our experience is that the pressure in a liquid or gas increases with depth. Referring to the beaker of liquid shown in Figure , the difference in pressure p between levels 0 and 1 arises because of the intervening liquid’s weight. With the two levels separated by depth h,the weight of the liquid column is –

w = ρgAh

where Ah is the enclosed volume.By using the free body diagram of Figure , the equilibrium-force balance of the liquid column shows that the pressure at depth 1 is

p1 = p0 + ρgh

Figure : Equilibrium of a beaker filled with liquid. Pressure increases with depth because of the weight of the fluid above

What is Pressure Force

The pressure grows in direct proportion to the depth and the density of the fluid. Similar to stress , pressure has the dimensions of force per-unit-area. In the SI, the unit of pressure is the pascal (1 Pa = 1 N/m^2), named after the seventeenth-century scientist and philosopher Blaise Pascal,who conducted chemical experiments involving air and other gases. The derived dimensions psi = lb/in2 (pounds per square inch) and psf = lb/ft2 (pounds per square foot) are generally used for pressure in the USCS, as is the unit of atmosphere (atm). Table 2 provides conversion factors between these conventional units. In the table’s first row, for instance,we see that the pascal is related to the other three dimensions as follows: 1 Pa = 1.450 x 10^-4 psi = 2.089 x 10^-2 psf  = 9.869 x 10^-6 atm .

Table 2 : Conversion Factors Between USCS and SI Units for Pressure

 

Practical examples of Buoyancy Forces

When ships are docked in port and hot air balloons hover above the ground, they are subjected to the buoyancy forces created by the surrounding fluid. As shown in Figure , when a submarine is submerged and floating at a steady depth, the net force on it is zero since the (upward) buoyancy force balances the submarine’s weight. The buoyancy force FB equals the weight of fluid displaced by an object according to the equation

FB = ρ (fluid) . g . V (object) = ρ . g . V

Figure : Buoyancy force acting  on                               a submerged submarine

where ρ  represents the fluid’s density, and V is the volume of fluid displaced by the object. Historically, this result is attributed to Archimedes, a Greek mathematician and inventor, who revealed the fraudulent of a goldsmith who manufactured a golden crown that had been commissioned by King Hieros II. The king suspected that the   dishonest goldsmith had replaced a portion of the crown’s gold with silver. Archimedes recognized that the principle embodied in Equation above could be used to determine whether the crown had been produced from pure gold or from a less dense (and less valuable) alloy of gold and silver.