Ray diagrams can be used to determine the image location, size, orientation and type of image formed of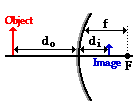 objects when placed at a given location in front of a mirror. The use of these diagrams was demonstrated earlier in Lesson 3 and in Lesson 4. Ray diagrams provide useful information about object-image relationships, yet fail to provide the information in a quantitative form. While a ray diagram may help one determine the approximate location and size of the image, it will not provide numerical information about image distance and image size. To obtain this type of numerical information, it is necessary to use the Mirror Equation and the Magnification Equation. The mirror equation expresses the quantitative relationship between the object distance (do), the image distance (di), and the focal length (f). The equation is stated as follows:
objects when placed at a given location in front of a mirror. The use of these diagrams was demonstrated earlier in Lesson 3 and in Lesson 4. Ray diagrams provide useful information about object-image relationships, yet fail to provide the information in a quantitative form. While a ray diagram may help one determine the approximate location and size of the image, it will not provide numerical information about image distance and image size. To obtain this type of numerical information, it is necessary to use the Mirror Equation and the Magnification Equation. The mirror equation expresses the quantitative relationship between the object distance (do), the image distance (di), and the focal length (f). The equation is stated as follows:
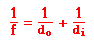
The magnification equation relates the ratio of the image distance and object distance to the ratio of the image height (hi) and object height (ho). The magnification equation is stated as follows:
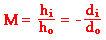
These two equations can be combined to yield information about the image distance and image height if the object distance, object height, and focal length are known. Their use was demonstrated in Lesson 3 for concave mirrors and will be demonstrated here for convex mirrors. As a demonstration of the effectiveness of the Mirror equation and Magnification equation, consider the following example problem and its solution.
Example Problem #1
A 4.0-cm tall light bulb is placed a distance of 35.5 cm from a convex mirror having a focal length of -12.2 cm. Determine the image distance and the image size.
Like all problems in physics, begin by the identification of the known information.
| ho = 4.0 cm | do = 35.5 cm | f = -12.2 cm |
Next identify the unknown quantities that you wish to solve for.
| di = ??? | hi = ??? |
To determine the image distance (di), the mirror equation will have to be used. The following lines represent the solution to the image distance; substitutions and algebraic steps are shown.
1/f = 1/do + 1/di
1/(-12.2 cm) = 1/(35.5 cm) + 1/di
-0.0820 cm-1 = 0.0282 cm-1 + 1/di
-0.110 cm-1 = 1/di
| di = -9.08 cm |
The numerical values in the solution above were rounded when written down, yet unrounded numbers were used in all calculations. The final answer is rounded to the third significant digit.
To determine the image height (hi), the magnification equation is needed. Since three of the four quantities in the equation (disregarding the M) are known, the fourth quantity can be calculated. The solution is shown below.
hi/ho = – di/do
hi /(4.0 cm) = – (-9.08 cm)/(35.5 cm)
hi = – (4.0 cm) • (-9.08 cm)/(35.5 cm)
| hi = 1.02 cm |
The negative values for image distance indicate that the image is located behind the mirror. As is often the case in physics, a negative or positive sign in front of the numerical value for a physical quantity represents information about direction. In the case of the image distance, a negative value always indicates the existence of a virtual image located behind the mirror. In the case of the image height, a positive value indicates an upright image. Further information about the sign conventions for the variables in the Mirror Equation and the Magnification Equation can be found in Lesson 3.
From the calculations in this problem it can be concluded that if a 4.0-cm tall object is placed 35.5 cm from a convex mirror having a focal length of -12.2 cm, then the image will be upright, 1.02-cm tall and located 9.08 cm behind the mirror. The results of this calculation agree with the principles discussed earlier in this lesson. Convex mirrors always produce images that are upright, virtual, reduced in size, and located behind the mirror.
ur Understanding
1. A convex mirror has a focal length of -10.8 cm. An object is placed 32.7 cm from the mirror’s surface. Determine the image distance.
See Answer

Answer: di = -8.1 cm
Use the equation 1 / f = 1 / do + 1 / di where f = -10.8 cm and do = + 32.7 cm
Substitute and solve for di.
2. Determine the focal length of a convex mirror that produces an image that is 16.0 cm behind the mirror when the object is 28.5 cm from the mirror.
See Answer

Answer: f = -36.6 cm
Use the equation 1 / f = 1 / do + 1 / di where do = 28.5 cm and di = -16.0 cm
(Careful: image distances for convex mirrors are always negative.)
Substitute and solve for f.
3. A 2.80-cm diameter coin is placed a distance of 25.0 cm from a convex mirror that has a focal length of -12.0 cm. Determine the image distance and the diameter of the image.
See Answer

Answer: di = -8.1 cm and hi = 0.909 cm
Use the equation 1 / f = 1 / do + 1 / di where f = -12.0 cm and do = +25.0 cm
Substitute and solve for di.
Then use hi / ho = – di / do where ho = 2.80 cm, do = +25 cm and di = -8.1 cm
Substitute and solve for hi.
4. A focal point is located 20.0 cm from a convex mirror. An object is placed 12 cm from the mirror. Determine the image distance.
See Answer

Answer: di = -7.5 cm
Use the equation 1 / f = 1 / do + 1 / di where f = – 20.0 cm and do = +12.0 cm
(Careful: convex mirrors have focal lengths which are negative.)
Substitute and solve for di.


