The emphasis of Lesson 1 of this unit is to present some evidence that has historically supported the view that light behaves as a wave. The reflection, refraction and diffraction of light waves is one strand of evidence. The interference of light waves is a second strand of evidence. In the early nineteenth century, Thomas Young showed that the interference of light passing through two slits produces an interference pattern when projected on a screen. In this section of Lesson 1, we will investigate another example of interference that provides further evidence in support of the wavelike behavior of light.

Perhaps you have witnessed streaks of color on a car windshield shortly after it has been swiped by a windshield wiper or a squeegee at a gas station. The momentary streaks of color are the result of interference of light by the very thin film of water or soap that remains on the windshield. Or perhaps you have witnessed streaks of color in a thin film of oil resting upon a water puddle or concrete driveway. These streaks of color are the result of the interference of light by the very thin film of oil that is spread over the water surface. This form of interference is commonly called thin film interference and provides another line of evidence for the wave behavior of light.

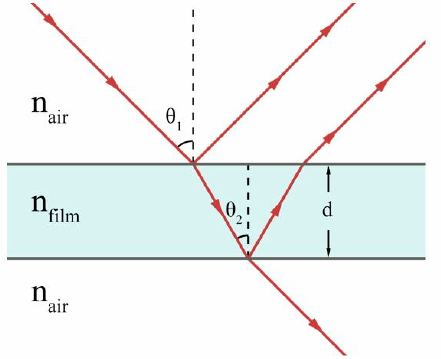
Light wave interference results when two waves are traveling through a medium and meet up at the same location. So what exactly is causing this thin film interference? What is the source of the two waves? When a wave (light waves included) reaches the boundary between two media, a portion of the wave reflects off the boundary and a portion is transmitted across the boundary. The reflected portion of the wave remains in the original medium. The transmitted portion of the wave enters the new medium and continues traveling through it until it reaches a subsequent boundary. If the new medium is a thin film, then the transmitted wave does not travel far before it reaches a new boundary and undergoes the usual 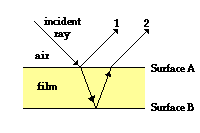reflection and transmission behavior. Thus, there are two waves that emerge from the film – one wave that is reflected off the top of the film (wave 1 in the diagram) and the other wave that reflects off the bottom of the film (wave 2 in the diagram).

These two waves could interfere constructively if they meet two conditions. One condition is that the two waves must be relatively close together such that their crests and troughs can meet up with each other and cause the interference. To meet this condition, the light must be incident at angles close to zero with respect to the normal. (This is not shown in the diagram above in order to space out the waves for clarity sake.) A second condition that must be met is that the wave that travels through the film and back into the original medium must have traveled just the right distance such that it is in phase with the other reflected wave. Two waves that are in phase are waves that are always at the same point on their wave cycle. That is, the two waves must be forming crests at the same location and at the same moment in time and forming troughs at the same location and at the same moment in time. In order for the second condition to occur, the thickness of the film must be just perfect.

If wave 1 and wave 2 meet these two conditions as they reflect and exit the film, then they will constructively interfere. As will be learned in Lesson 2, light that is visible to our eyes consists of a collection of light waves of varying wavelength. Each wavelength is characterized by its own color. So a red light wave has a different wavelength than an orange light wave that has a different wavelength than a yellow light wave. While the thickness of a film at a given location may not allow a red and an orange light wave to emerge from the film in phase, it may be just perfect to allow a yellow light wave to emerge in phase. So at a given location on the film, the yellow light wave undergoes constructive interference and becomes brighter than the other colors within the incident light. As such, the film appears yellow when viewed by incident sunlight. Other locations of the film may be just perfect to constructively reinforce red light. And still others area of the film may be of perfect thickness for the constructive reinforcement of green light. Because different locations of the film may be of appropriate thickness to reinforce different colors of light, the thin film will show streaks of color when viewed from above.

While the mathematics of thin film interference can become quite complicated, it is clear from this discussion that thin film interference is another phenomenon that can only be explained using a wave model of light.