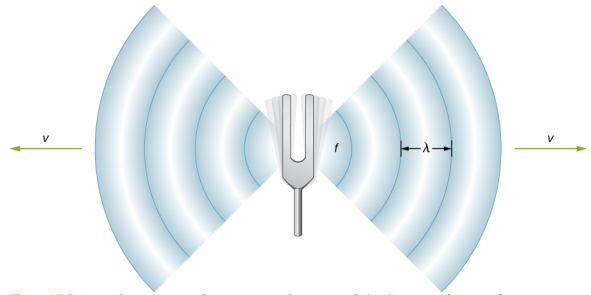
A sound wave is a pressure disturbance that travels through a medium by means of particle-to-particle interaction. As one particle becomes disturbed, it exerts a force on the next adjacent particle, thus disturbing that particle from rest and transporting the energy through the medium. Like any wave, the speed of a sound wave refers to how fast the disturbance is passed from particle to particle. While frequency refers to the number of vibrations that an individual particle makes per unit of time, speed refers to the distance that the disturbance travels per unit of time. Always be cautious to distinguish between the two often-confused quantities of speed (how fast…) and frequency (how often…).

Since the speed of a wave is defined as the distance that a point on a wave (such as a compression or a rarefaction) travels per unit of time, it is often expressed in units of meters/second (abbreviated m/s). In equation form, this is

 

speed = distance/time

The faster a sound wave travels, the more distance it will cover in the same period of time. If a sound wave were observed to travel a distance of 700 meters in 2 seconds, then the speed of the wave would be 350 m/s. A slower wave would cover less distance – perhaps 660 meters – in the same time period of 2 seconds and thus have a speed of 330 m/s. Faster waves cover more distance in the same period of time.

Factors Affecting Wave Speed

The speed of any wave depends upon the properties of the medium through which the wave is traveling. Typically there are two essential types of properties that affect wave speed – inertial properties and elastic properties. Elastic properties are those properties related to the tendency of a material to maintain its shape and not deform whenever a force or stress is applied to it. A material such as steel will experience a very small deformation of shape (and dimension) when a stress is applied to it. Steel is a rigid material with a high elasticity. On the other hand, a material such as a rubber band is highly flexible; when a force is applied to stretch the rubber band, it deforms or changes its shape readily. A small stress on the rubber band causes a large deformation. Steel is considered to be a stiff or rigid material, whereas a rubber band is considered a flexible material. At the particle level, a stiff or rigid material is characterized by atoms and/or molecules with strong attractions for each other. When a force is applied in an attempt to stretch or deform the material, its strong particle interactions prevent this deformation and help the material maintain its shape. Rigid materials such as steel are considered to have a high elasticity. (Elastic modulus is the technical term). The phase of matter has a tremendous impact upon the elastic properties of the medium. In general, solids have the strongest interactions between particles, followed by liquids and then gases. For this reason, longitudinal sound waves travel faster in solids than they do in liquids than they do in gases. Even though the inertial factor may favor gases, the elastic factor has a greater influence on the speed (v) of a wave, thus yielding this general pattern:

v_solids > v_liquids > v_gases

Inertial properties are those properties related to the material’s tendency to be sluggish to changes in its state of motion. The density of a medium is an example of an inertial property. The greater the inertia (i.e., mass density) of individual particles of the medium, the less responsive they will be to the interactions between neighboring particles and the slower that the wave will be. As stated above, sound waves travel faster in solids than they do in liquids than they do in gases. However, within a single phase of matter, the inertial property of density tends to be the property that has a greatest impact upon the speed of sound. A sound wave will travel faster in a less dense material than a more dense material. Thus, a sound wave will travel nearly three times faster in Helium than it will in air. This is mostly due to the lower mass of Helium particles as compared to air particles.

 

The Speed of Sound in Air

The speed of a sound wave in air depends upon the properties of the air, mostly the temperature, and to a lesser degree, the humidity. Humidity is the result of water vapor being present in air. Like any liquid, water has a tendency to evaporate. As it does, particles of gaseous water become mixed in the air. This additional matter will affect the mass density of the air (an inertial property). The temperature will affect the strength of the particle interactions (an elastic property). At normal atmospheric pressure, the temperature dependence of the speed of a sound wave through dry air is approximated by the following equation:

v = 331 m/s + (0.6 m/s/C)•T

where T is the temperature of the air in degrees Celsius. Using this equation to determine the speed of a sound wave in air at a temperature of 20 degrees Celsius yields the following solution.

v = 331 m/s + (0.6 m/s/C)•T

v = 331 m/s + (0.6 m/s/C)•(20 C)

v = 331 m/s + 12 m/s

v = 343 m/s

(The above equation relating the speed of a sound wave in air to the temperature provides reasonably accurate speed values for temperatures between 0 and 100 Celsius. The equation itself does not have any theoretical basis; it is simply the result of inspecting temperature-speed data for this temperature range. Other equations do exist that are based upon theoretical reasoning and provide accurate data for all temperatures. Nonetheless, the equation above will be sufficient for our use as introductory Physics students.)

Using Wave Speed to Determine Distances

At normal atmospheric pressure and a temperature of 20 degrees Celsius, a sound wave will travel at approximately 343 m/s; this is approximately equal to 750 miles/hour. While this speed may seem fast by human standards (the fastest humans can sprint at approximately 11 m/s and highway speeds are approximately 30 m/s), the speed of a sound wave is slow in comparison to the speed of a light wave. Light travels through air at a speed of approximately 300 000 000 m/s; this is nearly 900 000 times the speed of sound. For this reason, humans can observe a detectable time delay between the thunder and the lightning during a storm. The arrival of the light wave from the location of the lightning strike occurs in so little time that it is essentially negligible. Yet the arrival of the sound wave from the location of the lightning strike occurs much later. The time delay between the arrival of the light wave (lightning) and the arrival of the sound wave (thunder) allows a person to approximate his/her distance from the storm location. For instance if the thunder is heard 3 seconds after the lightning is seen, then sound (whose speed is approximated as 345 m/s) has traveled a distance of

distance = v • t = 345 m/s • 3 s = 1035 m

If this value is converted to miles (divide by 1600 m/1 mi), then the storm is a distance of 0.65 miles away.

Another phenomenon related to the perception of time delays between two events is an echo. A person can often perceive a time delay between the production of a sound and the arrival of a reflection of that sound off a distant barrier. If you have ever made a holler within a canyon, perhaps you have heard an echo of your holler off a distant canyon wall. The time delay between the holler and the echo corresponds to the time for the holler to travel the round-trip distance to the canyon wall and back. A measurement of this time would allow a person to estimate the one-way distance to the canyon wall. For instance if an echo is heard 1.40 seconds after making the holler, then the distance to the canyon wall can be found as follows:

distance = v • t = 345 m/s • 0.70 s = 242 m

The canyon wall is 242 meters away. You might have noticed that the time of 0.70 seconds is used in the equation. Since the time delay corresponds to the time for the holler to travel the round-trip distance to the canyon wall and back, the one-way distance to the canyon wall corresponds to one-half the time delay.

While an echo is of relatively minimal importance to humans, echolocation is an essential trick of the tradefor bats. Being a nocturnal creature, bats must use sound waves to navigate and hunt. They produce short bursts of ultrasonic sound waves that reflect off objects in their surroundings and return. Their detection of the time delay between the sending and receiving of the pulses allows a bat to approximate the distance to surrounding objects. Some bats, known as Doppler bats, are capable of detecting the speed and direction of any moving objects by monitoring the changes in frequency of the reflected pulses. These bats are utilizing the physics of the Doppler effect discussed in an earlier unit (and also to be discussed later in Lesson 3). This method of echolocation enables a bat to navigate and to hunt.

The Wave Equation Revisited

Like any wave, a sound wave has a speed that is mathematically related to the frequency and the wavelength of the wave. As discussed in a previous unit, the mathematical relationship between speed, frequency and wavelength is given by the following equation.

Speed = Wavelength • Frequency

Using the symbols v, λ, and f, the equation can be rewritten as

v = f • λ

The above equation is useful for solving mathematical problems related to the speed, frequency and wavelength relationship. However, one important misconception could be conveyed by the equation. Even though wave speed is calculated using the frequency and the wavelength, the wave speed is not dependent upon these quantities. An alteration in wavelength does not affect (i.e., change) wave speed. Rather, an alteration in wavelength affects the frequency in an inverse manner. A doubling of the wavelength results in a halving of the frequency; yet the wave speed is not changed. The speed of a sound wave depends on the properties of the medium through which it moves and the only way to change the speed is to change the properties of the medium.

 

Check Your Understanding

1. An automatic focus camera is able to focus on objects by use of an ultrasonic sound wave. The camera sends out sound waves that reflect off distant objects and return to the camera. A sensor detects the time it takes for the waves to return and then determines the distance an object is from the camera. If a sound wave (speed = 340 m/s) returns to the camera 0.150 seconds after leaving the camera, how far away is the object?

See Answer

Answer = 25.5 m

The speed of the sound wave is 340 m/s. The distance can be found using d = v • t resulting in an answer of 25.5 m. Use 0.075 seconds for the time since 0.150 seconds refers to the round-trip distance.

2. On a hot summer day, a pesky little mosquito produced its warning sound near your ear. The sound is produced by the beating of its wings at a rate of about 600 wing beats per second.

a. What is the frequency in Hertz of the sound wave?

b. Assuming the sound wave moves with a velocity of 350 m/s, what is the wavelength of the wave?

See Answer

Part a Answer: 600 Hz (given)

Part b Answer: 0.583 meters

Let  = wavelength. Use v = f • λ where v = 350 m/s and f = 600 Hz. Rearrange the equation to the form of λ = v / f. Substitute and solve.

3. Doubling the frequency of a wave source doubles the speed of the waves.

a. True

b. False

See Answer

Answer: B

Doubling the frequency will halve the wavelength; speed is unaffected by the alteration in the frequency. The speed of a wave depends upon the properties of the medium.

4.Playing middle C on the piano keyboard produces a sound with a frequency of 256 Hz. Assuming the speed of sound in air is 345 m/s, determine the wavelength of the sound corresponding to the note of middle C.

See Answer

 Answer: 1.35 meters (rounded)

Let λ = wavelength. Use v = f • λ where v = 345 m/s and f = 256 Hz. Rearrange the equation to the form of λ = v / f. Substitute and solve.

5. Most people can detect frequencies as high as 20 000 Hz. Assuming the speed of sound in air is 345 m/s, determine the wavelength of the sound corresponding to this upper range of audible hearing.

See Answer

Answer: 0.0173 meters (rounded)

Let λ = wavelength. Use v = f • λ where v = 345 m/s and f = 20 000 Hz. Rearrange the equation to the form of λ = v / f. Substitute and solve.

6. An elephant produces a 10 Hz sound wave. Assuming the speed of sound in air is 345 m/s, determine the wavelength of this infrasonic sound wave.

See Answer

Answer: 34.5 meters

Let λ = wavelength. Use v = f • λ where v = 345 m/s and f = 10 Hz. Rearrange the equation to the form of λ = v / f. Substitute and solve.

7. Determine the speed of sound on a cold winter day (T=3 degrees C).

See Answer

Answer: 332.8 m/s

The speed of sound in air is dependent upon the temperature of air. The dependence is expressed by the equation:

v = 331 m/s + (0.6 m/s/C) • T

where T is the temperature in Celsius. Substitute and solve.

v = 331 m/s + (0.6 m/s/C) • 3 C

v = 331 m/s + 1.8 m/s

v = 332.8 m/s

8. Miles Tugo is camping in Glacier National Park. In the midst of a glacier canyon, he makes a loud holler. He hears an echo 1.22 seconds later. The air temperature is 20 degrees C. How far away are the canyon walls?

See Answer

Answer = 209 m

The speed of the sound wave at this temperature is 343 m/s (using the equation described in the Tutorial). The distance can be found using d = v • t resulting in an answer of 343 m. Use 0.61 second for the time since 1.22 seconds refers to the round-trip distance.

9. Two sound waves are traveling through a container of unknown gas. Wave A has a wavelength of 1.2 m. Wave B has a wavelength of 3.6 m. The velocity of wave B must be __________ the velocity of wave A.

a. one-ninth	b. one-third
c. the same as	d. three times larger than

See Answer

Answer: C

The speed of a wave does not depend upon its wavelength, but rather upon the properties of the medium. The medium has not changed, so neither has the speed.

close

10. Two sound waves are traveling through a container of unknown gas. Wave A has a wavelength of 1.2 m. Wave B has a wavelength of 3.6 m. The frequency of wave B must be __________ the frequency of wave A.

a. one-ninth	b. one-third
c. the same as	d. three times larger than

See Answer

Answer: B

Since Wave B has three times the wavelength of Wave A, it must have one-third the frequency. Frequency and wavelength are inversely related.