According to Varignon’s theorem, the algebraic sum of several concurrent forces about any point is equal to the moments of the moments of their resultant about the point.
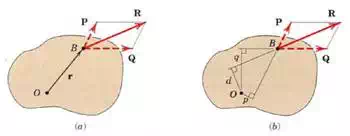
To prove Varignon’s Theorem, consider the force R acting in the plane of the body as shown in the above left side figure(a). The forces ”P and ‘Q’ represent any two non rectangular components of ‘R’. The moment of ‘R’ about point ‘O’ is
Mo = r*R
Because R = P + Q, we can write
r*R = r*(P + Q)
Using the distributive law for cross products, we have
Mo = r*R = r*P + r*Q
which says that the moment of ‘R’ about ‘O’ equals the sum of the moments about ‘O’ of its components ‘P’ and ‘Q’. This proves the theorem.
Varignon’s theorem need not be restricted to the case of two components, but it applies equally well to three or more. Thus we could have used any number of concurrent components of R in the foregoing proof.
In the above right side figure(b) illustrates the usefulness of Varignon’s theorem. The moment of ‘R’ about point ‘O’ is R*d. However, if ‘d’ is more difficult to determine than ‘p’ and ‘q’, we can resolve ‘R’ into the components ‘P’ and ‘Q’, and compute the moment as
Mo = R*d = – p*P + q*Q
where we take the clockwise moment sense to he positive.