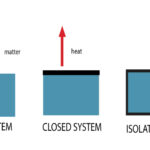
If a system is not isolated, then the total system momentum is not conserved. To understand this concept, we will return to our original analogy. Suppose Jack and Jill (each with $100 in their pockets) undergo a financial interaction in which Jack hands Jill $50 for the purchase of some goods. If Jack and Jill were isolated from the influence of the rest of the world, then Jack would end up with $50 and Jill would end up with $150. The total money in the system would be $200 both before and after the transaction; total system money would be conserved. If however, a third influence enters from outside of the system to take away or (more fortunately) to add money to the system, then total system momentum would not be conserved. If a thief interfered with his filthy hands so as to steal $20, then perhaps Jack would finish with $40 and Jill would finish with $140. In the case of a non-isolated system, the total system momentum is not conserved.

Because of the inevitability of friction and air resistance in any real collision, one can conclude that no system is ever perfectly isolated. The reasoning is that there will always be a resistance force of some kind robbing the system of its momentum. For this reason, the law of conservation of momentum must be some sort of pie-in-the-sky idea that never has any applicability. Why does one ever need to learn a law that is always broken?

We friends of physics would quickly agree that resistance forces such as friction and air resistance are inevitable. However, one must be careful of overrating the impact of such forces on total system momentum. To illustrate, consider the collision between two 1000-kg cars – one that is initially at rest and one that is moving at 10 m/s (approximately 22 mi/hr). Such a collision would last for a fraction of a second. Suppose the actual contact forces between cars occur for 0.01 seconds. Perhaps after this very short 0.01 seconds, the cars stick together and slide a short distance across the asphalt street. For such a realistic collision, a typical contact force might be close to 500 000 N. A typical friction force would be no larger than 10 000 N (and would probably be considerably less). Each force would deliver an impulse to the vehicles during the collision in order to change the momentum of the colliding vehicles. The 500 000 N contact force between vehicles is an internal force and does not serve to change the momentum of the system. The 10 000 N friction force is an external force and would alter the total system momentum by approximately 200 kg•m/s (100 kg•m/s for each car). This loss of system momentum must be compared to the total system momentum of 10 000 kg•m/s. In this very realistic case, friction would cause no more than a 2% loss of total system momentum. If the collision being analyzed involved objects with even greater speeds, the percent loss of total system momentum would be considerably less.

So one must again consider the charge that the law of conservation of momentum is a pie-in-the-sky idea. The best response is to say that it is a very accurate model approximating the exchange of momentum between colliding objects. In the collision just described, the worse case scenario is that the assumption of momentum conservation is 98% accurate. Because contact forces during collisions are so large compared to the inevitable resistance forces such as friction and air resistance, the law of momentum conservation is a great tool for analyzing collisions and providing an accurate estimate of a post-collision (or a pre-collision) speed. In the next part of Lesson 2, the power of this conservation model to predict pre- and post-collision speeds of colliding objects will be illustrated.