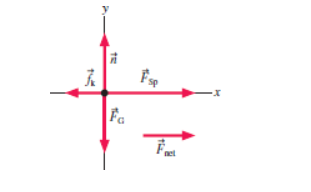
Since acceleration is a vector quantity, it has a direction associated with it. The direction of the acceleration vector depends on two things:

·         whether the object is speeding up or slowing down

·         whether the object is moving in the + or – direction

The general principle for determining the acceleation is:

If an object is slowing down, then its acceleration is in the opposite direction of its motion.

This general principle can be applied to determine whether the sign of the acceleration of an object is positive or negative, right or left, up or down, etc. Consider the two data tables below. In each case, the acceleration of the object is in the positive direction. In Example A, the object is moving in the positive direction (i.e., has a positive velocity) and is speeding up. When an object is speeding up, the acceleration is in the same direction as the velocity. Thus, this object has a positive acceleration. In Example B, the object is moving in the negative direction (i.e., has a negative velocity) and is slowing down. According to our general principle, when an object is slowing down, the acceleration is in the opposite direction as the velocity. Thus, this object also has a positive acceleration.

This same general principle can be applied to the motion of the objects represented in the two data tables below. In each case, the acceleration of the object is in the negative direction. In Example C, the object is moving in the positive direction (i.e., has a positive velocity) and is slowing down. According to ourprinciple, when an object is slowing down, the acceleration is in the opposite direction as the velocity. Thus, this object has a negative acceleration. In Example D, the object is moving in the negative direction (i.e., has a negative velocity) and is speeding up. When an object is speeding up, the acceleration is in the same direction as the velocity. Thus, this object also has a negative acceleration.

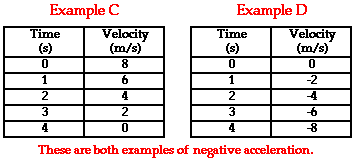
Observe the use of positive and negative as used in the discussion above (Examples A – D). In physics, the use of positive and negative always has a physical meaning. It is more than a mere mathematical symbol. As used here to describe the velocity and the acceleration of a moving object, positive and negative describe a direction. Both velocity and acceleration are vector quantities and a full description of the quantity demands the use of a directional adjective. North, south, east, west, right, left, up and down are all directional adjectives. Physics often borrows from mathematics and uses the + and – symbols as directional adjectives. Consistent with the mathematical convention used on number lines and graphs, positive often means to the right or up and negative often means to the left or down. So to say that an object has a negative acceleration as in Examples C and D is to simply say that its acceleration is to the left or down (or in whatever direction has been defined as negative). Negative accelerations do not refer acceleration values that are less than 0. An acceleration of -2 m/s/s is an acceleration with a magnitude of 2 m/s/s that is directed in the negative direction