As an object moves, it often undergoes changes in speed. For example, during an average trip to school, there are many changes in speed. Rather than the speed-o-meter maintaining a steady reading, the needle constantly moves up and down to reflect the stopping and starting and the accelerating and decelerating. One instant, the car may be moving at 50 mi/hr and another instant, it might be stopped (i.e., 0 mi/hr). Yet during the trip to school the person might average 32 mi/hr. The average speed during an entire motion can be thought of as the average of all speedometer readings. If the speedometer readings could be collected at 1-second intervals (or 0.1-second intervals or … ) and then averaged together, the average speed could be determined. Now that would be a lot of work. And fortunately, there is a shortcut. Read on.

The average speed during the course of a motion is often computed using the following formula:

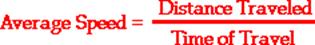
In contrast, the average velocity is often computed using this formula

Let’s begin implementing our understanding of these formulas with the following problem:

Q: While on vacation, Lisa Carr traveled a total distance of 440 miles. Her trip took 8 hours. What was her average speed?

To compute her average speed, we simply divide the distance of travel by the time of travel.

That was easy! Lisa Carr averaged a speed of 55 miles per hour. She may not have been traveling at a constant speed of 55 mi/hr. She undoubtedly, was stopped at some instant in time (perhaps for a bathroom break or for lunch) and she probably was going 65 mi/hr at other instants in time. Yet, she averaged a speed of 55 miles per hour. The above formula represents a shortcut method of determining the average speed of an object.