and minimum normal stresses

                                                            ii.      Can be found out by taking derivative of with respect the angle  and we will get

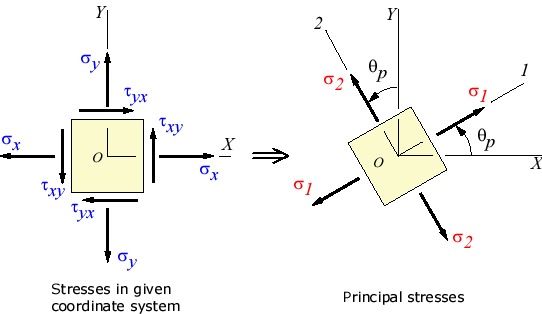
1.      This  has two values differ by 90^o they are known as principal angles.

2.      They also represent orientation of planes known as principal planes.

3.      One value of angle represents maximum stress and other minimum stress.

4.      From 1^st point we can say that principal stresses occur on mutually perpendicular axes    

                                                          iii.      Substituting the values of  in the original equation we will get the value of maximum and minimum normal stress i.e.  respectively

 is maximum or minimum  = 0

F The principal planes for elements in uniaxial stress and biaxial stress are the x and y planes themselves.

F For an element in pure shear, the principal planes are oriented at 45° to the x axis

b.    Maximum Shear stress

                                                              i.      Like principal stress we can find out maximum shear stress also. By taking derivative of with respect the angle  and we will get

1.      This  has two values differ by 90^o

2.      The maximum and minimum values only differ by sign the magnitude is same

3.      Comparing the formulae of  and   we get

The above equation shows that the planes of maximum shear stress occur at 45° to the principal planes

                                                            ii.      Substituting the values of  in the original equation we will get the value of maximum

                                                          iii.      There is one alternate expression for 

F  Normal stresses have same value when  is maximum or minimum i.e. 

F In the particular cases of uniaxial stress and biaxial stress the planes of maximum shear stress occur at 45° to the x and y axes.

F In the case of pure shear the maximum shear stresses occur on the x and y planes