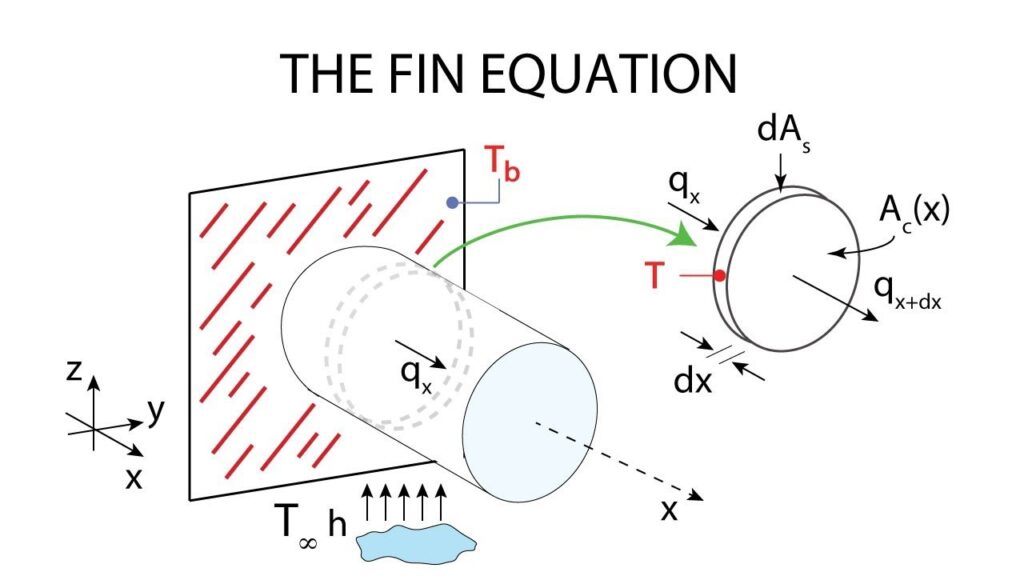
1)    Assumptions

a)      Steady operation with no heat generation

b)      Thermal conductivity k of the material to remain constant.

c)      Convection heat transfer coefficient h to be constant and uniform over the entire surface of the fin

i)        The value of h is usually much lower at the fin base than it is at the fin tip because the fluid is surrounded by solid surfaces near the base, which seriously disrupt its motion to the point of “suffocating” it.

ii)      Adding too many fins on a surface may actually decrease the overall heat transfer when the decrease in h offsets any gain resulting from the increase in the surface area.

2)       

		θ is Temperature excess
The General Solution for the above differential equation isSince there are two coefficient hence we will need at least 2 boundary condition

3)      Different Cases in Fins

	Infinitely long Fin	Insulated Fin tip	Specified temperature at fin tip	Convection at fin tip
1st Boundary Condition	At Fin base at x=0
2nd Boundary Condition
Temperature Distribution
Heat transfer from entire fin

4)      Fin efficiency

5)      Fin Effectiveness

When determining the rate of heat transfer from a finned surface, we must consider the unfinned portion of the surface as well as the fins. Therefore the rate of heat transfer for a surface containing n fins can be expressed as

a)      The thermal conductivity k of the fin material should be as high as possible. Thus it is no coincidence that fins are made from metals, with copper, aluminum, and iron being the most common ones. Perhaps the most widely used fins are made of aluminum because of its low cost and weight and its resistance to corrosion.

b)      The ratio of the perimeter to the cross-sectional area of the fin p/A_c should be as high as possible. This criterion is satisfied by thin plate fins and slender pin fins.

c)      

i)        mL = 5  ® an infinitely long fin

ii)      mL= 1 offer a compromise between heat transfer performance and the fin size