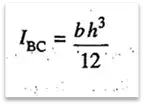Moment of Inertia – It may be defined as the moment of the moment i.e. second moment of mass or area of a body. It is usually denoted by I.

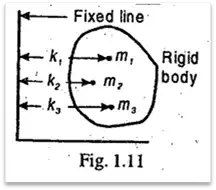
Consider a body of total mass m. Let it is composed of small particles of masses m1, m2, m3 etc. If k1, k2, k3 etc, are the distances from a fixed line, as shown in Fig. 1.11, then mass moment of inertia of the whole body is given by

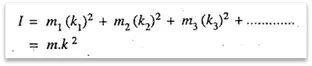
If, instead of mass, the area of the figure is taken into consideration, then moment of inertia of the area is given by

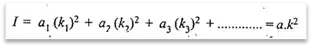
where k is theradius of gyration. It is defined as the distance from a given reference where the whole mass or area of the body is assumed to be concentrated to give the same value of I.

In S.I. units, the unit of mass moment of inertia is kg-m2 and the moment of inertia of the area 

is expressed in m4 or mm4.

If the moment of inertia of a body about an axis passing through its center of gravity (i.e. IG) is 

known, then the moment of inertia about any other parallel axis (i.e. Ip) may be obtained by using 

parallel axis theorem.

According to parallel axis theorem, the moment of inertia about a parallel axis,

The following are the values of I for simple cases :

1. The moment of inertia of a thin disc of mass m and radius r, about an axis passing through its center of gravity and perpendicular to the plane of the disc is

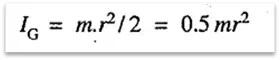
and moment of inertia about a diameter,

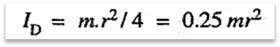
2. The moment of inertia of a thin rod of mass m and length l, about an axis passing through its centre of gravity and perpendicular to its length is

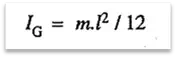
and moment of inertia about a parallel axis through one end of the rod,

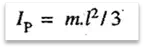
3. The moment of inertia of a rectangular section having width b and depth d as shown in 

Fig.1.12, is given by

4. The moment of inertia of a hollow rectangular section, as shown in figure 1.13 is given by

5. The moment of inertia of a circular section of diameter D as shown in Fig. 1.14, is’given by

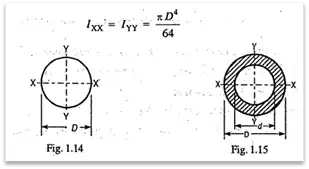
6. The moment of inertia of a hollow circular section of outer diameter D and inner diameter d, as shown in Fig. 1.15, is given by

7. The moment of inertia of a triangular section of height h, about an axis passing through its center of gravity G and parallel to the base BC, as shown in Fig. 1.16, is given by

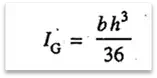
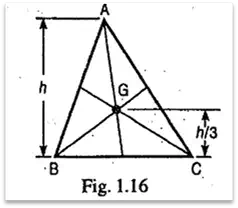
and moment of inertia about the base BC,