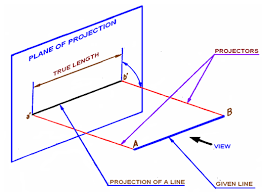
Problem-1 Projection of Straight Lines – A line AB, 60 mm long, is inclined at an angle of 450 to HP. and 300 to VP. One of its end point A is in HP as well as VP. Determine its apparent inclinations.

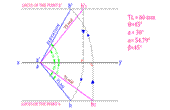
Procedure:

Step-1 Draw a horizontal line, which is x-y line of some suitable length.

Step-2 Mark a point a’ &  a on a common point on the x-y line.

Step-3 Draw a line a’b’1 from the point a’, above & at an angle 45°, which is represented by the letter θ,  with the x-y line as shown into the figure.

Step-4 Draw a line ab2 from the point a, below & at an angle of 30°, which is represented by the letter Φ, with the x-y line.

Step-5 From the end points of these previously drawn lines (i.e. b’1 & b2 ) draw horizontal lines which are parallel with the line x-y.

Step-6 From the point b’1 draw a vertical line up to the x-y line in downward direction and perpendicular to the line x-y. Now make an arc with the point a’ as center and radius equal to the distance of the point of intersection of the previously drawn vertical line with  the x-y line, which will cut the horizontal line passing through the point b2. And give the name of that point b.

Step-7 Now draw a line between the points a & b, which is the plan of the line AB. Find its inclination with the x-y line, which is represented by the letter β.

Step-8 From the point b2 draw a vertical line up to the x-y line in upward direction and perpendicular to the line x-y. Now make an arc with the point  a  as center and radius equal to the distance of the point of intersection of the previously drawn vertical line with  the x-y line, which will cut the horizontal line passing through the point b’1. And give the name of that point b’.

Step-9 Now draw a line between the points a’ & b’, which is the elevation of the line AB. Find its inclination with the x-y line, which is represented by the letter α.

Step-10 Give the dimensions by any one method of dimensions and give the notations as shown into the figure. And make a list of the True Length & Angles made by the line AB as shown into the figure.