The idlers are an important part of a belt conveyor system; they provide stability to the conveyed materials. There are mainly three types of idles used in the industry namely, flat idlers, trough idlers, and garland idlers. In this article we will discuss only the flat type belt conveyor idler design.

The Basics of Flat Idler Design

Typically, the following inputs are used for starting up the design process of the flat idler:

○      Capacity of the conveyor generally expressed in tons per hour.

○      Bulk density of the conveyed materials generally expressed in tons per cubic meter.

○      Conveyor belt width generally expressed in meters.

○      Belt speed generally expressed in meters.

The output aims from the design process are:

○      The spacing of the idlers generally expressed in meters.

○      The idler speed generally expressed in meters per second.

○      Load on each idlers.

○      Idler diameter generally expressed in meters.

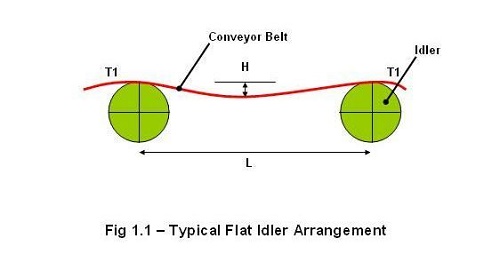
The following design equations are used across the industry for calculating the different design parameters of the flat idlers:

○      Spacing of the idlers

S = (8*T1*H)/ (mb+ml)*g…………..1.1

Where,

S is in meters

T1= Belt tension near the idlers as shown in the picture (N)

H=Belt sag (m)

mb = weight of the belt (kg/m)

ml =Weight of the conveyed material (kg/m)

g =Acceleration due to gravity

○      The weight of the conveyed material can be further calculated as

ml= (10*W)/ (36*V)…………1.2

Where,

mb is in kg/m.

W = Capacity of the conveyor (tons per hour)

V = Belt speed (m/sec)

○      Idler speed

N = (60*V)/ (Π*D)……………1.3

Where,

N is in RPM.

V = Belt speed (m/sec)

D = Diameter of the idlers

Loads on each idlers

○      F= (10*W*S*g)/ (36*V)…………1.4

Where,

F is in Newtons

g = Acceleration due to gravity

W = Capacity of the conveyor (tones per hour)

S = Spacing between the two idlers.

V = Belt speed (m/sec)

○      Maximum bending stress on the idlers

b= (8*F*L)/ (3*Π*D3)………………..1.5

Where,

b is in Newtons per square meter

F = loads on each idlers (Newton)

L = length of the idlers (Meter)

D = diameter of the idlers (meter)

One Practical Belt Conveyor Idler Design Example

Now, let’s see how to use the basic design equations for actual design purpose. We will take the following data as input:

Capacity of the conveyor W = 1000 t/h

Belt speed V =1.68 m/sec

Belt tension near idler T1=50000 N

Idler length L =1.2 m

Belt sag = 0.015 m

Weight of the belt mb=15 kg/m

Idler speed N= 50 rpm

Design procedure:

○      First, we will calculate the weight of the conveyed material using the eqn.1.2 as:

ml = (10*1000)/(36*1.68) = 165.34 kg/m

○      Now, to calculate the spacing between the two idlers we will use the eqn.1.1

S=(8*50000*0.015)/(15+165.34)*9.81 = 3.391 m

○      The diameter of the idler can be calculated from the eqn.1.3 as below:

D= (60*1.68)/ (3.14*50) = 0.64 m

○      Total load acted on each idler can be obtained from the eqn.1.4 :

F=(10*1000*3.391*9.81)/(36*1.68)=5500 N

○      Maximum bending stress applied on each idlers can be obtained from the eqn.1.5 as below:

b= (8*5500*1.2)/ (3*3.14*0.643) = 21385.176 N/m2

If the maximum bending stress calculated from the above equations is higher than the accepted limit of the bending stress then, you have to reconsider the input assumed parameters, for example you may have to set the lower idler speed or you have to think of the lower belt sag value, so that idler spacing got reduced and so the load per idler.

Conclusion

There are three types of idlers used in the conveyor industry, out of which only the flat belt conveyor idler design calculations are discussed here theoretically. We have not used the factor of safety in the design calculations here, or in other words the factor of safety is considered as one throughout the calculations. The theoretical calculations are ideal for the preliminary design. FEA tools like Ansys or Pro Mechanica should be used for the final virtual validation of the design.