In recent years, nanostructural carbon materials have received considerable interest from the scientific community due to their superior properties. Among carbon-based nanomaterials, single-layered graphene sheet (SLGS) is defined as a flat monolayer of carbon atoms tightly packed into a two-dimensional honeycomb lattice, in which carbon atoms bond covalently with their neighbors [1,2]. Graphene sheets (GSs) possess extraordinary properties, such as strong mechanical strength (Young’s modulus = 1.0 TPa), large thermal conductivity (thermal conductivity = 3000
W/KmW/Km
), excellent electric conductivity (electric conductivity up to 6000
S/cmS/cm
), high surface area, and unusual optical properties [3–5]. These unique properties have made GSs one of the most promising materials in many applications such as nanosensors, nano-electronics, nanocomposites, batteries, nano-oscillators, nano-actuators, nanoresonators, nano-optomechanical systems, supercapacitors, fuel cells, solar cells, and hydrogen storage [6, 7]. On the other hand, polyvinylidene fluoride (PVDF) is a piezoelectric polymer. It has superior properties, such as excellent dimensional stability, abrasion and corrosion resistance, high strength, and capability of maintaining its mechanical properties at elevated temperature [8]. In contrast to GS, PVDF is a smart material, since it has piezoelectric property. The specific characteristic of piezoelectric materials is their ability to produce an electric field when deformed, and undergo deformation when subjected to an electric field. The coupling nature of piezoelectric materials has wide applications in electromechanical and electric devices, such as electromechanical actuators, sensors, and transducers [9].
Understanding mechanical behaviors of GSs is a key step for designing many nano-electromechanical system (NEMS) devices. Especially, stability response of GSs as NEMS component has great importance. Many studies have been carried out on the basis of nonlocal elasticity theory, which was initiated in the papers of Eringen [10–12]. He regarded the stress state at a given point as a function of the strain states of all points in the body, while the local continuum mechanics assumes that the stress state at a given point depends uniquely on the strain state at the same point. Pradhan and Murmu [13] studied small-scale effect on the buckling analysis of SLGS embedded in an elastic medium based on nonlocal plate theory. They found that the buckling loads of SLGS are strongly dependent on the small-scale coefficients and the stiffness of the surrounding elastic medium. Explicit analytical expressions for the critical buckling stresses in a monolayer GS based on nonlocal elasticity were investigated by Ansari and Rouhi [14]. They concluded that with the appropriate selection of the nonlocal parameter, the nonlocal relations are capable of yielding excellent results from the static deflection of monolayer GS under a uniformly distributed load. Also, their results showed that the importance of the small length scale is dependent on the boundary conditions of monolayer GS. Akhavan et al. [15] introduced exact solutions for the buckling analysis of rectangular Mindlin plates subjected to uniformly and linearly distributed in-plane loading on two opposite edges simply supported resting on elastic foundation. Their results indicated that the buckling load parameter increases as the thickness-to-length ratio decreases. Hashemi and Samaei [16] proposed an analytical solution for the buckling analysis of rectangular nanoplates based on the nonlocal Mindlin plate theory. They graphically presented the effects of small length scale on buckling loads for different geometrical parameters.
Samaei et al. [17] employed nonlocal Mindlin plate theory to analyze buckling of SLGS embedded in an elastic medium. They found that the effects of small length scale and surrounding elastic medium are significant to the mechanical behavior of nanoplates or SLGS and cannot be ignored. Furthermore, they showed that the nonlocal assumptions present larger buckling loads and stiffness of elastic medium in comparison to classical plate theory. With respect to developmental works on mechanical behavior analysis of SLGS, it should be noted that none of the research mentioned above [13–17] have considered coupled double-nanoplate system. Herein, Murmu and Adhikari [18] analyzed nonlocal vibration of bonded double-nanoplate systems. Their study highlighted that the small-scale effects considerably influence the transverse vibration of NDNPS. Besides, they elucidated that the increase of the stiffness of the coupling springs in nonlocal double-nanoplate system (NDNPS) reduces the small-scale effects during the asynchronous modes of vibration. Also, nonlocal buckling behavior of bonded double-nanoplate system was studied by Murmu et al. [19] who showed that the nonlocal effects in coupled system are higher with increasing values of the nonlocal parameter for the case of synchronous buckling modes than in the asynchronous buckling modes. Moreover, their analytical results indicated that the increase of the stiffness of the coupling springs in the double-GS system reduces the nonlocal effects during the asynchronous modes of buckling. Both papers [18, 19] have considered Winkler model for simulation of elastic medium between two nanoplates. In this simplified model, a proportional interaction between pressure and deflection of SLGSs is assumed, which is carried out in the form of discrete and independent vertical springs. Whereas, Pasternak suggested considering not only the normal stresses but also the transverse shear deformation and continuity among the spring elements, and its subsequent applications for developing the model for buckling analysis proved to be more accurate than the Winkler model. To the best of our knowledge, none of works in the literature have taken into account the Pasternak model for coupled system. This study aims to couple SLGS with PVDF nanoplate by an elastic medium which is simulated by the Pasternak model.
The use of smart materials has received considerable attention due to their higher potential applicability for the mechanical behavior control in various research areas. These materials can produce control forces to structural elements according to the applied voltage. A number of researchers utilized the piezoelectric materials to control mechanical behavior. For example, analysis of composite plates with piezoelectric actuators for vibration controls using layerwise displacement theory was performed by Han and Lee [20]. Piezoelectric control of composite plate vibration was carried out by Pietrzakowski [21], who considered effect of electric potential distribution. Recently, Liao et al. [22] examined nonlinear vibration of the piezoelectric nanobeams based on the nonlocal theory by considering external voltage. They assumed an electric potential as a combination of cosine and linear variation. They observed that the positive/negative voltage decreases/increases the linear and nonlinear frequencies of the nanobeam. None of the aforementioned studies [20–22] have considered a nanostructure (e.g., SLGS) whose vibrational behavior is controlled by an elastically bonded smart material (e.g., PVDF nanoplate).
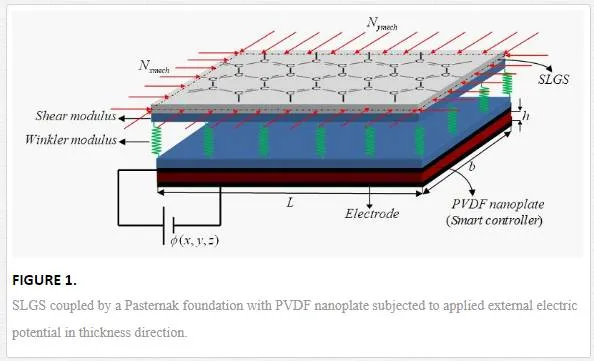
However, to date, no report has been found in the literature on buckling analysis and smart control of SLGS using elastically coupled PVDF nanoplate based on nonlocal Mindlin plate theory. Motivated by these considerations, in order to improve optimum design of nanostructures, we aim to investigate the buckling smart control of SLGS based on nonlocal Mindlin plate theory. Herein, SLGS is elastically coupled with PVDF nanoplate and controlled by applying external electric voltage in thickness direction of PVDF nanoplate. The influences of external electric voltage, small-scale parameter, elastic medium, length of SLGS, and axial half wave number on buckling behavior of SLGS have been taken into account.
Review of nonlocal piezoelasticity and Mindlin plate theory
NONLOCAL PIEZOELASTICITY
Based on the theory of nonlocal piezoelasticity, the stress tensor and the electric displacement at a reference point depend not only on the strain components and electric-field components at same position but also on all other points of the body. The nonlocal constitutive behavior for the piezoelectric material can be given as follows [22]:
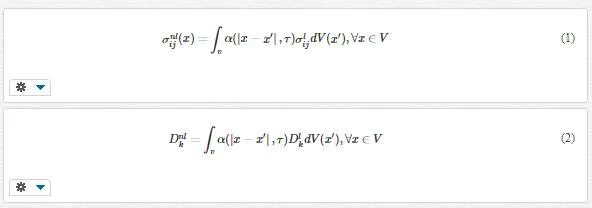


MINDLIN PLATE THEORY
Based on the Mindlin plate theory, the displacement field can be expressed as [15–17]:

Modeling of the problem

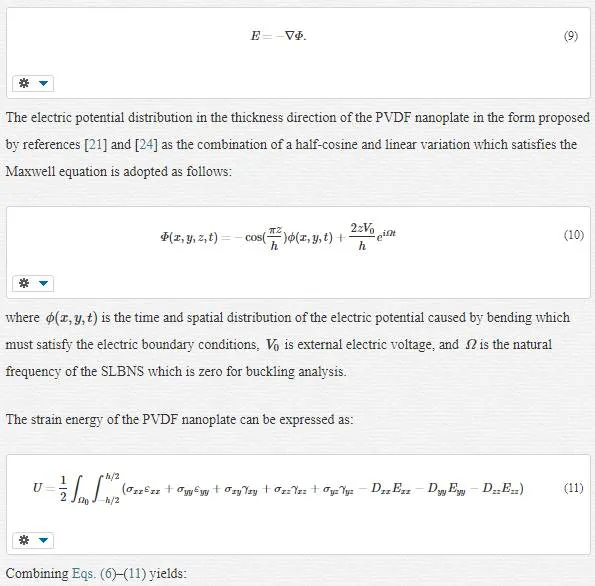
CONSTITUTIVE RELATIONS FOR PVDF NANOPLATE




in which
KK
is shear correction coefficient.
The external work due to surrounding elastic medium can be written as:




CONSTITUTIVE RELATIONS FOR SLGS
The SLGS is subjected to uniform compressive edge loading along x and y axis. In order to obtain the governing equations of SLGS, the procedure outlined above for PVDF nanoplate can be expressed repeatedly by ignoring piezoelectric coefficient in Eq. (7) and electric displacement (Eq. (8)).

It is noted that the superscript PVDF nanoplate in section 3.1 can be changed to GS in this section.
Solution procedure
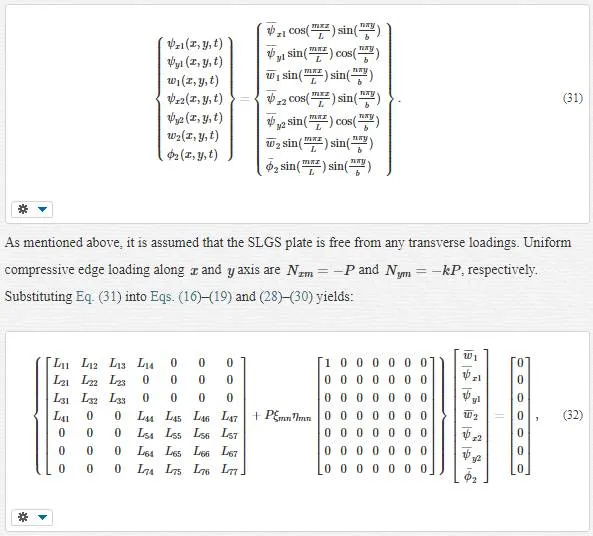
Steady-state solutions to the governing equations of the plate motion and the electric potential distribution which relate to the simply supported boundary conditions and zero electric potential along the edges of the surface electrodes can be assumed as [17,21]:
Numerical results
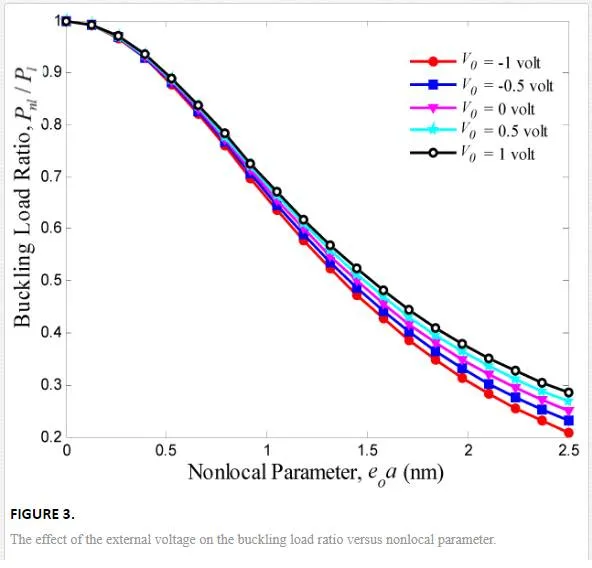
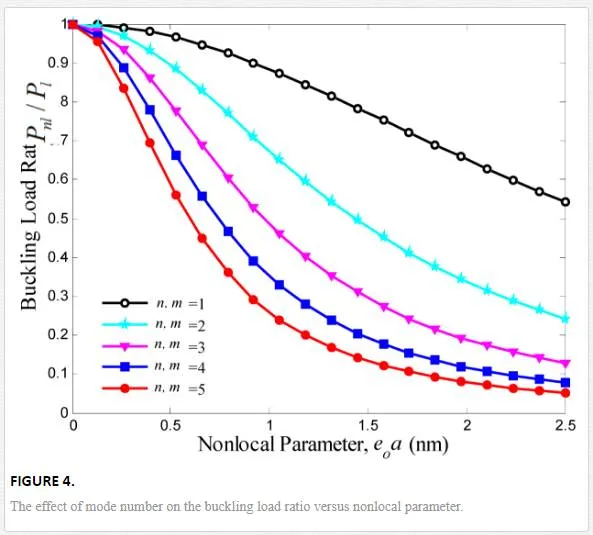
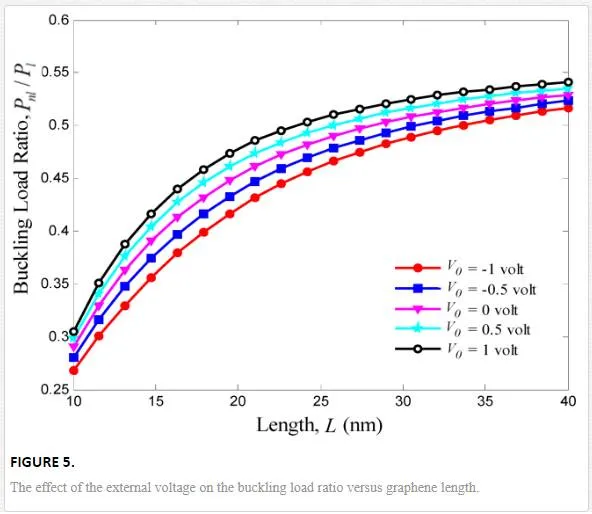
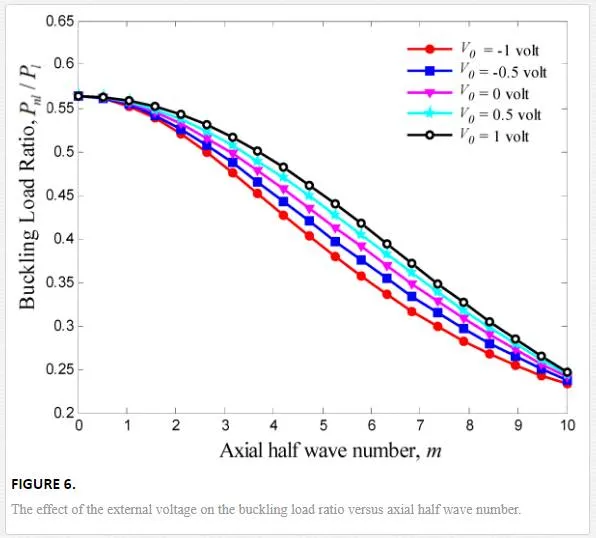
In this section, buckling smart control of SLGS using elastically bonded PVDF nanoplate is discussed so that the effects of nonlocal parameter, mode number, Pasternak foundation, and SLGS length on the buckling of the SLGS are also considered. For this purpose, buckling load ratio is defined as follows:

The orthotropic mechanical properties of SLGS with thickness
h=0.34nmh=0.34nm
are listed in Table 1 [25]. Also, mechanical and electrical characteristics of PVDF nanoplate with thickness
h=2nmh=2nm
are presented in Table 1 [26], which are taken from the macroscopic piezoelectric materials. In fact, the polymeric piezoelectric nanomaterials’ characteristics are size-dependent and determined by experiments or molecular dynamic (MD) simulation [22]. To the best of the author’s knowledge, the experimental values of piezoelectric nanomaterials’ properties are not available in the literature. Therefore, in order to quantitatively analyze the present work, the characteristics of PVDF nanoplate are assumed in macroscale.
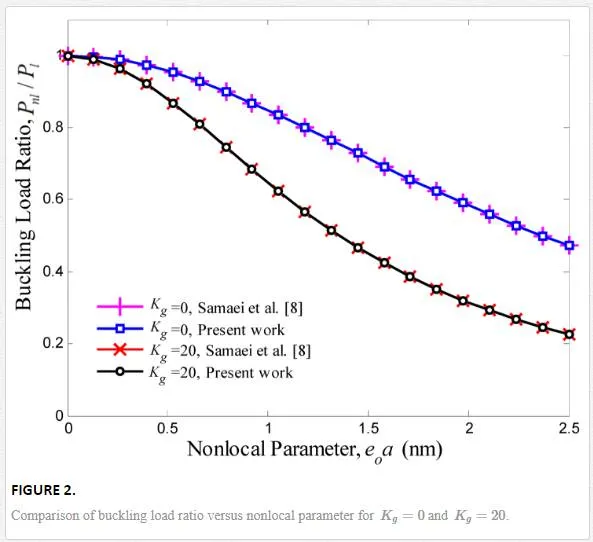
The developed nonlocal theory to date is incapable of determining the small scaling parameter
e0ae0a
. However, Eringen [11] proposed
e0a=0.39nme0a=0.39nm
by matching the dispersion curves using nonlocal theory for plane waves and Born–Karman model of lattice dynamics. For CNT, the
e0ae0a
is found to be less than
2nm2nm
[27]. Small-scale effects on the buckling behavior of SLGS and PVDF nanoplate were carried out analytically by assuming a range of values
0<e0a<2nm0<e0a<2nm
, since its exact value is not known [27].


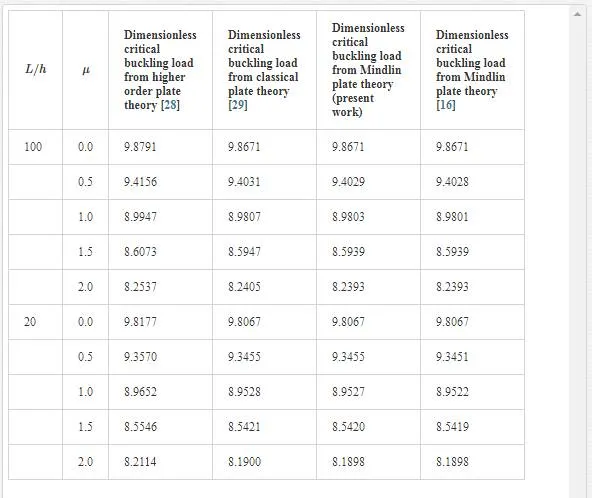
.

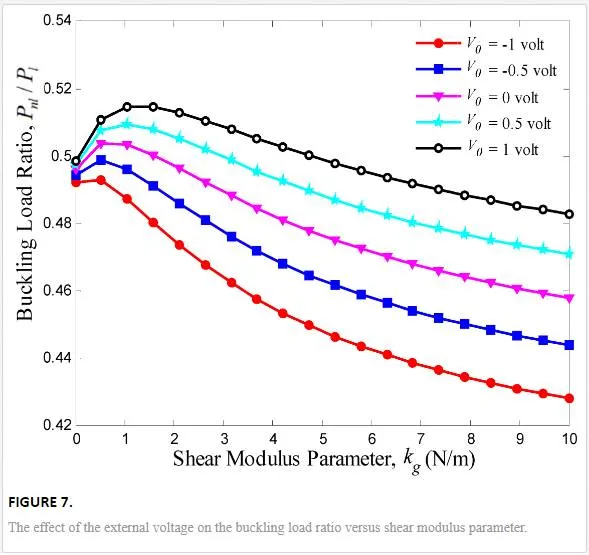
Conclusion
Buckling response of graphene sheets has applications in designing many NEMS/MEMS devices such as strain sensor, mass and pressure sensors, and atomic dust detectors. Buckling smart control of the SLGS using elastically bonded PVDF nanoplate which is subjected to external voltage is the main contribution of the present paper. The elastic medium between SLGS and PVDF nanoplate is simulated by a Pasternak foundation. The governing equations are obtained based on nonlocal Mindlin plate theory so that the effects of small-scale, elastic medium coefficient, mode number, and graphene length are discussed. The results indicate that the imposed external voltage is an effective controlling parameter for buckling of the SLGS. It is found that the effect of external voltage becomes more prominent at higher nonlocal parameter and shear modulus. It is also observed that for a given length, the SLGS with negative external voltage will buckle first as compared to the SLGS with positive one. The results of this study are validated as far as possible by the buckling of SLGS in the absence of PVDF nanoplate, as presented by [16, 17, 28, and 29]. Finally, it is hoped that the results presented in this paper would be helpful for study and design of bonded systems based on smart control and electromechanical systems.


