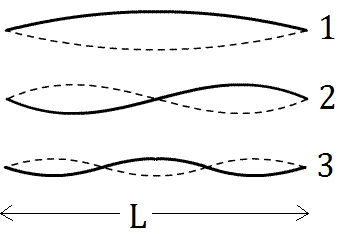
As discussed in Lesson 4, standing wave patterns are wave patterns produced in a medium when two waves of identical frequencies interfere in such a manner to produce points along the medium that always appear to be standing still. Such standing wave patterns are produced within the medium when it is vibrated at certain frequencies. Each frequency is associated with a different standing wave pattern. These frequencies and their associated wave patterns are referred to as harmonics. A careful study of the standing wave patterns reveal a clear mathematical relationship between the wavelength of the wave that produces the pattern and the length of the medium in which the pattern is displayed. Furthermore, there is a predictability about this mathematical relationship that allows one to generalize and deduce a statement concerning this relationship. To illustrate, consider the first harmonic standing wave pattern for a vibrating rope as shown below.

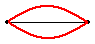
Analyzing the First Harmonic Pattern

The pattern for the first harmonic reveals a single antinode in the middle of the rope. This antinode position along the rope vibrates up and down from a maximum upward displacement from rest to a maximum downward displacement as shown. The vibration of the rope in this manner creates the appearance of a loop within the string. A complete wave in a pattern could be described as starting at the rest position, rising upward to a peak displacement, returning back down to a rest position, then descending to a peak downward displacement and finally returning back to the rest position. The animation below depicts this familiar pattern. As shown in the animation, one complete wave in a standing wave pattern consists of two loops. Thus, one loop is equivalent to one-half of a wavelength.

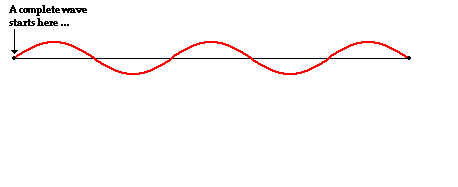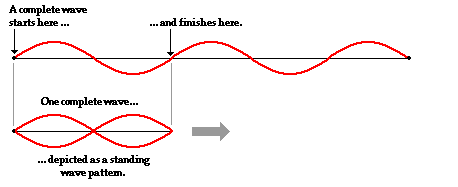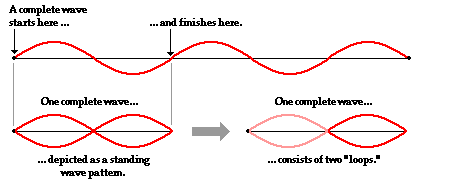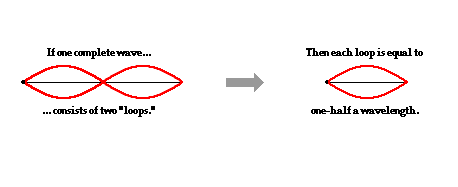
In comparing the standing wave pattern for the first harmonic with its single loop to the diagram of a complete wave, it is evident that there is only one-half of a wave stretching across the length of the string. That is, the length of the string is equal to one-half the length of a wave. Put in the form of an equation:

Analyzing the Second Harmonic Pattern

Now consider the string being vibrated with a frequency that establishes the standing wave pattern for the second harmonic.

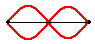
The second harmonic pattern consists of two anti-nodes. Thus, there are two loops within the length of the string. Since each loop is equivalent to one-half a wavelength, the length of the string is equal to two-halves of a wavelength. Put in the form of an equation:

The same reasoning pattern can be applied to the case of the string being vibrated with a frequency that establishes the standing wave pattern for the third harmonic.

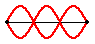
Analyzing the Third Harmonic Pattern

The third harmonic pattern consists of three anti-nodes. Thus, there are three loops within the length of the string. Since each loop is equivalent to one-half a wavelength, the length of the string is equal to three-halves of a wavelength. Put in the form of an equation:

When inspecting the standing wave patterns and the length-wavelength relationships for the first three harmonics, a clear pattern emerges. The number of antinodes in the pattern is equal to the harmonic number of that pattern. The first harmonic has one antinode; the second harmonic has two antinodes; and the third harmonic has three antinodes. Thus, it can be generalized that the nth harmonic has n antinodes where n is an integer representing the harmonic number. Furthermore, one notices that there are n halves wavelengths present within the length of the string. Put in the form of an equation:

Summarizing the Mathematical Relationships

This information is summarized in the table below.

Harmonic	Pattern	# of Loops	Length-WavelengthRelationship
1st		1	L = 1 / 2 • λ
2nd		2	L = 2 / 2 • λ
3rd		3	L = 3 / 2 • λ
4th		4	L = 4 / 2 • λ
5th		5	L = 5 / 2 • λ
6th		6	L = 6 / 2 • λ
nth	—	n	L = n / 2 • λ

For standing wave patterns, there is a clear mathematical relationship between the length of a string and the wavelength of the wave that creates the pattern. The mathematical relationship simply emerges from the inspection of the pattern and the understanding that each loop in the pattern is equivalent to one-half of a wavelength. The general equation that describes this length-wavelength relationship for any harmonic is:

Test your understanding of this relationship by answering the questions below.

 

 Check Your Understanding

1. Suppose that a string is 1.2 meters long and vibrates in the first, second and third harmonic standing wave patterns. Determine the wavelength of the waves for each of the three patterns.

See Answer

First harmonic: 2.4 m

Second harmonic: 1.2 m

Third harmonic: 0.8 m

For the first harmonic, the length of the string is equivalent to one-half of a wavelength. If the string is 1.2 meters long, then one-half of a wavelength is 1.2 meters long. The full wavelength is 2.4 meters long.

For the second harmonic, the length of the string is equivalent to a full wavelength. If the string is 1.2 meters long, then the wavelength is 1.2 meters long.

For the third harmonic, the length of the string is equivalent to three-halves of a wavelength. If the string is 1.2 meters long, then 1.5 wavelengths is 1.2 meters long. A single wavelength is less than 1.2 meters; it can be found by dividing 1.2 meters by 1.5. The wavelength of the third harmonic is 0.8 meters.

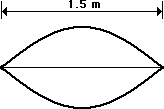2. The string at the right is 1.5 meters long and is vibrating as the first harmonic. The string vibrates up and down with 33 complete vibrational cycles in 10 seconds. Determine the frequency, period, wavelength and speed for this wave.

See Answer

Given: L = 1.5 m

33 cycles in 10 seconds

The frequency refers to how often a point on the medium undergoes back-and-forth vibrations; it is measured as the number of cycles per unit of time. In this case, it is

f = (33 cycles) / (10 seconds) = 3.3 Hz

The period is the reciprocal of the frequency.

T = 1 / (3.3 Hz) = 0.303 seconds

The wavelength of the wave is related to the length of the rope. For the first harmonic as pictured in this problem, the length of the rope is equivalent to one-half of a wavelength. That is, L = 0.5 • W where W is the wavelength. Rearranging the equation and substituting leads to the following results:

W = 2 • L = 2 • (1.5 m) = 3.0 m

The speed of a wave can be calculated from its wavelength and frequency using the wave equation:

v = f • W = (3.3 Hz) • (3. 0 m) = 9.9 m/s

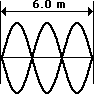3. The string at the right is 6.0 meters long and is vibrating as the third harmonic. The string vibrates up and down with 45 complete vibrational cycles in 10 seconds. Determine the frequency, period, wavelength and speed for this wave.

See Answer

Given: L = 6.0 m

45 cycles in 10 seconds

The frequency refers to how often a point on the medium undergoes back-and-forth vibrations; it is measured as the number of cycles per unit of time. In this case, it is

f = (45 cycles) / (10 seconds) = 4.5 Hz

The period is the reciprocal of the frequency.

T = 1 / (4.5 Hz) = 0.222 seconds

The wavelength of the wave is related to the length of the rope. For the third harmonic as pictured in this problem, the length of the rope is equivalent to three-halves of a wavelength. That is, L = 1.5 • W where W is the wavelength. Rearranging the equation and substituting leads to the following results:

W = (2 / 3) • L = (2 / 3) • (6.0 m) = 4.0 m

The speed of a wave can be calculated from its wavelength and frequency using the wave equation:

v = f • W = (4.5 Hz) • (4. 0 m) = 18 m/s

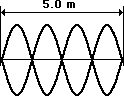4. The string at the right is 5.0 meters long and is vibrating as the fourth harmonic. The string vibrates up and down with 48 complete vibrational cycles in 20 seconds. Determine the frequency, period, wavelength and speed for this wave.

See Answer

Given: L = 5.0 m

48 cycles in 20 seconds

The frequency refers to how often a point on the medium undergoes back-and-forth vibrations; it is measured as the number of cycles per unit of time. In this case, it is

f = (48 cycles) / (20 seconds) = 2.4 Hz

The period is the reciprocal of the frequency.

T = 1 / (2.4 Hz) = 0.417 seconds

The wavelength of the wave is related to the length of the rope. For the fourth harmonic as pictured in this problem, the length of the rope is equivalent to two full wavelengths. That is, L = 2 • W where W is the wavelength. Rearranging the equation and substituting leads to the following results:

W = 0.5 • L = 0.5 • (5.0 m) = 2.5 m

The speed of a wave can be calculated from its wavelength and frequency using the wave equation:

v = f • W = (2.4 Hz) • (2.5 m) = 6.0 m/s

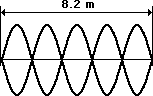5. The string at the right is 8.2 meters long and is vibrating as the fifth harmonic. The string vibrates up and down with 21 complete vibrational cycles in 5 seconds. Determine the frequency, period, wavelength and speed for this wave.

See Answer

 

Given: L = 8.2 m

21 cycles in 5 seconds

The frequency refers to how often a point on the medium undergoes back-and-forth vibrations; it is measured as the number of cycles per unit of time. In this case, it is

f = (21 cycles) / (5 seconds) = 4.2 Hz

The period is the reciprocal of the frequency.

T = 1 / (4.2 Hz) = 0.238 seconds

The wavelength of the wave is related to the length of the rope. For the fifth harmonic as pictured in this problem, the length of the rope is equivalent to five-halves of a wavelength. That is, L = w.5 • W where W is the wavelength. Rearranging the equation and substituting leads to the following results:

W = (2 / 5) • L = (2 / 5) • (8.2 m) = 3.28 m

The speed of a wave can be calculated from its wavelength and frequency using the wave equation:

v = f • W = (4.2 Hz) • (3.28 m) = 13.8 m/s